Mathe Gleichungen Brüche?
weiß jemand wie man Aufgabe g) rechnet denn ich komm irgendwie nicht weiter dass Ergebnis muss -9 sein es wäre natürlich schön mit einer Erklärung und den Rechen weg !
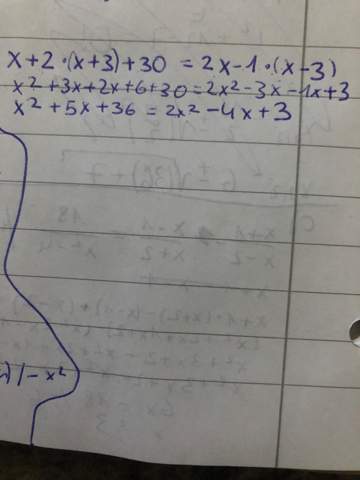
Ich habe versucht weiterzureichen ist es so richtig wenn ja wie soll ich weiter vorgehen dass 2x hoch 2 verwirrt mich
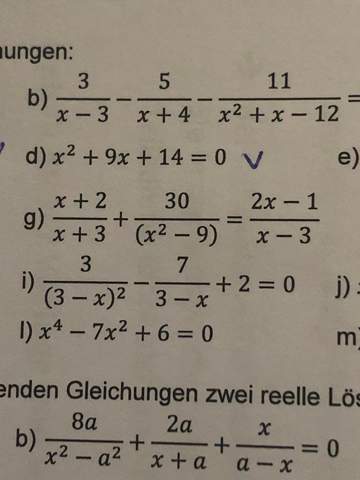
6 Antworten
(x+2)/(x+3)+30/(x²-9)=(2x-1)/(x-3)
x ≠ -3 und x ≠ +3
Doch noch nicht alles richtig
klar? Diesmal bekommst du es
komplett. Da in diesem Modus
mehr Platz gebraucht wird als
sonst, teile ich es in linke
und rechte Seite vom
Gleichheitszeichen.
Erst mal der Hauptnenner:
Da (x²-9) = (x+3)*(x-3)ist
(3. Binomisches Gesetz),
erweitere ich alle Brüche so,
dass sie auf den Hauptnenner
kommen. (Macht man meist durch
Überlegung im Kopf.)
Linke Seite:
(x+2)(x-3)/((x+3)(x-3))+30/(x²-9)
= (x²-x-6)/(x²-9) + 30/(x²-9)
Rechte Seite:
(2x-1)(x+3)/((x-3)(x+3)
= (2x²+5x-3) / (x²-9)
Du siehst, es steht überall
(x²-9) im Nenner, also
multipliziere ich die ganze
Gleichung miz (x²-9) und kürze
sofort wieder mit dem vorhandenen
Nenner. Die Nenner sind dann weg.
Am besten, du schreibst dir
diesen Vorgang mit richtigen
Bruchstrichen ins Heft.
Jedenfalls steht da nur noch:
x² - x - 6 + 30 = 2x² + 5x - 3
Die ganze rechte Seite muss
nach links:
-x² - 6x + 27 = 0 | *(-1)
x² + 6x - 27 = 0
Das kannst du?
Eine der beiden Lösungen ist -9.
den Hauptnenner finden und auf diesen bringen, dann einfach zusammen fassen.
Bei Hauptnenner finden: schau dir mal den Nenner des zweiten Bruches an und erinnere dich an die dritte binomische Formel.
Indem Du sämtliche Brüche mit (x²-9) erweiterst. Dann verschwindet im mittleren Bruch der Nenner; im linken Bruch wird der Zähler um (x-3) erweitert; analog im rechten.
Bedenke:
(x+3)* (x-3) =x² - 9.
Indem Du konventionell weitermachst: Alle x und x² auf eine Seite bringen.
Probiere aus, ob das funktioniert:
Ersetzen von (x²-9) = (x-3)(x+3)
Dann gesamte Gleichung multiplizieren mit (x-3)(x+3)
Definitionsmenge beachten: D = R \ {-3 ; 3}
Hauptnenner: (x + 3) * (x - 3)
Und wie rechne ich dann weiter nachdem ich es so gemacht habe ?