Mathe - Gleichung richtig Probe falsch?
Hallo, es geht um folgende Aufgabe:
(x+1)/(x-1) = (2x+1)/(2x+3)
Als Ergebnis erhalte ich immer und immer wieder -2/3. Laut einem online- Rechner ist das auch richtig.
Doch die Probe ergibt: -19/6=4/3
Also stimmt da doch etwas nicht. Aber was? Kann mir bitte jemand helfen ich verzweilfe schon..
3 Antworten
Wenn etwas über oder unter einem Bruchstrich stehen soll, du aber keinen echten Bruchstrich zur vefügung hast, musst Du den Zähler und den Nenner jeweils in Klammern schreiben, sonst kann keiner Deine Frage beantworten.
Was da steht, ist:
x+(1/x)-1 = 2x+(1/2x)+3
Die Gleichung lautet wohl:
(x+1)/(x-1) = (2x+1)/(2x+3)
Und die Lösung ist tatsächlich -2/3.
Die Probe liefert auf beiden Seiten -1/5.
Ich verstehe die Rechnung wie ihr beiden auf das Ergebnis der Probe kommt. Ich weiß wohl nichts mehr aus der Schule und stehe noch dazu auf dem Schlauch :(
Also bei mir stimmt auch die Probe...
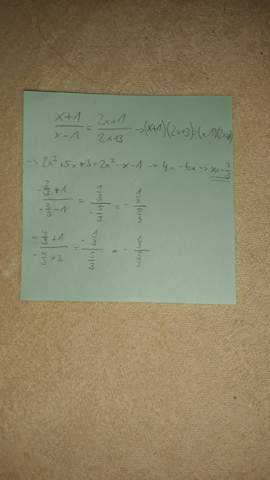
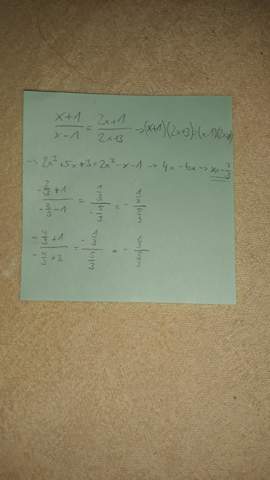
Naja, einfach den Wert für x einsetzen und durchrechnen (oder an einer geeigneten Stelle aufhören).
Wie kommst du auf die (1/3)/(-5/3) ? Das verstehe ich gerde üerhaupt nicht.
Genau wie ich oben beschrieben habe. X ersetzt und dann die Werte ausgerechnet.
Und warum sind (-4/3)+3 = (5/3) ? Ich stehe immer noch auf dem Schlauch
Wow danke, sieht sinnvoll aus. Dann verstehe ich anscheinend nicht, wie die Probe funktioniert :(