Mathe GFS - Brennpunkt einer Parabel?
Hallo,
wie sollte ich am Besten meine GFS halten also in welcher Reihenfolge? Ich versteh das Thema zudem nicht ganz. Hat jemand Tipps und kann mir helfen? Wäre sehr dankbar!
Habt ihr schon das Thema Ableitungen?
Ja, wir hatten schon Ableitung, Tangente, Normale. Also alles was man dafür bräuchte.
1 Antwort
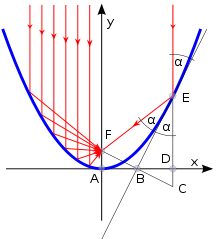
Der Brennpunkt hat die besondere Eigenschaft, dass alle zur y-Achse parallelen Geraden von der Parabel durch diesen Punkt reflektiert werden.
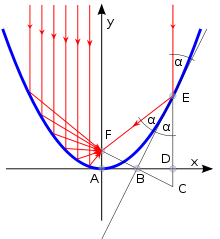
Man kann sich schnell klarmachen, dass der Brennpunkt auf der Symmetrie-Achse der Parabel liegen muss.
Haben wir also eine Scheitelpunktform einer quadratischen Funktion gegeben (oder formen sie zu dieser um), also
f(x) = a (x – b)² + c,
muss der Brennpunkt als B(x|y) als x-Koordinate die Stelle x = b haben.
Wie kommen wir aber auf die y-Koordinate?
Wir wissen, dass die Tangentengleichung an einer Stelle x₀ gerade
t(x) = f(x₀) + f'(x₀) (x – x₀)
ist. Nun betrachten wir den Winkel Alpha, der zwischen der Tangente und der an der Stelle x₀ zur y-Achse parallelen Gerade liegt. (Siehe auch Bild oben.)
Den Winkel Alpha kann man mit
Alpha = 90° – arctan( f'(x₀) )
berechnen - zumindestens solange wir im ersten Quadranten sind.
Aus der Physik weißt du vielleicht noch, dass für einen Lichtstrahl gilt
"Einfallswinkel = Ausfallswinkel".
Die zur y-Achse parallelen Gerade an der Stelle x₀ wird also von der Tangente an der Stelle x₀ mit dem Ausfallswinkel Alpha reflektiert. Das entspricht einer Geraden mit der Steigung
m = tan( 90° – 2 Alpha )
m = tan( 90° – 2 (90° – arctan( f'(x₀) )
m = tan( 2 arctan( f'(x₀) ) – 90° ).
Die Gerade sieht also so aus:
g(x) = m (x – x₀) + f(x₀).
Wir müssen jetzt noch den Schnittpunkt dieser Geraden mit der Symmetrie-Achse berechnen, dann haben wir unseren Brennpunkt. Wir wissen ja schon, dass die Symmetrie-Achse an der Stelle b liegt, also berechnen wir einfach g(b).
g(b) = m (b – x₀) + f(x₀)
g(b) = tan( 2 arctan( f'(x₀) ) – 90° ) (b – x₀) + f(x₀).
Wir können, da der Brennpunkt für alle x₀ gilt, einfach eine beliebige Stelle (außer b) einsetzen und erhalten unseren Brennpunkt B(b|g(b)).
Jetzt kannst du eine beliebige quadratische Funktion definieren und ihren Brennpunkt bestimmen. Hier das Beispiel mit der Normalparabel:
f(x) = x² => f'(x) = 2 x.
Es ist also b = 0. Wir setzen x₀ = 1.
g(0) = tan( 2 arctan(2) – 90°) (–1) + 1²
g(0) = 0,25.
Unser Brennpunkt ist also B(0|0,25).
Tatsächlich hat der Brennpunkt einer Parabel der Form ax² immer die Koordinaten B(0|1/(4a)).
Da präsentierst du dem Fragenden ja praktisch seine halbe GFS auf dem Silberteller .....