Mathe Aufgabe?
Hallo,kann mir jemand helfen,wie berechne ich das?

2 Antworten
Da eine Seite und der Umfang gegeben ist, kann man alle Seitenlängen berechnen. Der Kosinussatz liefert dann die Länge der senkrechten Leiste.
In dem Dreieck, das die linke Hälfte des Drachens bildet, kennt man die Seiten a = AB und b = BD und den eingeschlossenen Winkel Beta. (D soll die untere Spitze des Drachens sein.) Man kann den Flächeninhalt dieses Dreiecks ABD berechnen:
A = 1/2 * a * b * sin(Beta)
Sei e die Länge der senkrechten Leiste und f die Länge der waagerechten Leiste. Wenn e Grundseite und f/2 Höhe im Dreieck ABD ist, dann ist
A = 1/2 * e * f/2, also
a * b * sin(Beta) = e * f/2
Damit kann man f ausrechnen.
Geg.: Schnurlänge Ls = 2,65 m = 265 cm
Geg.: a = 51 cm ; β = 95,9°
---
b = (Ls - (2 * a)) / 2
b = (265 - (2 * 51)) / 2
b = 81,5 cm
---
e = WURZEL( a² + b² - 2 * a * b * cos(β) )
e = WURZEL( 51^2 + 81,5^2 - 2 * 51 * 81,5 * cos(95,9) )
e = 100,487632 cm rd. 1 m
Senkrechte Leiste beträgt 1 m (100 cm).
---
f = ( a * SIN(α/2) ) * 2
f = ( 51 * SIN(53,77949) ) * 2
f = 82,28838 rd. 82 cm
Waagrechte Leiste beträgt 82 cm
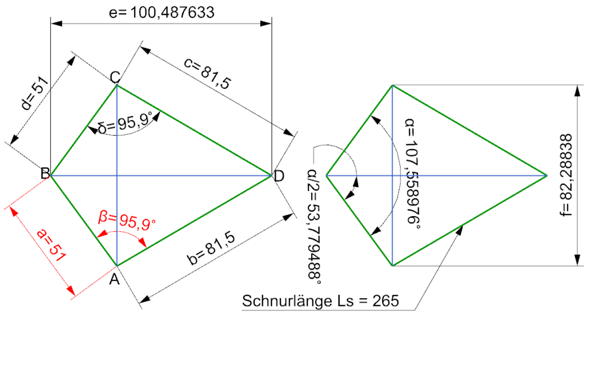

Und wie würde ich jetzt die waagerechte berechnen?