Logarithmen umwandeln in Numerus?
Hey für den ein oder anderen mag meine Frage echt dumm sein, aber wie bekomme ich es hin aus einem Logarithmus den Numerus zu gewinnen also die umkehr Funktion von einer Zahl die ich zum Logarithmus mache. ein Beispiel falls ihr mich nicht ganz verstanden habt. log 30 = 1.47712125... wie geht nun die Umkehroperation also log^-1 1.47712125 = 30. auf meinem Taschenrechner hab ich leider die log^-1 Taste nicht.
4 Antworten
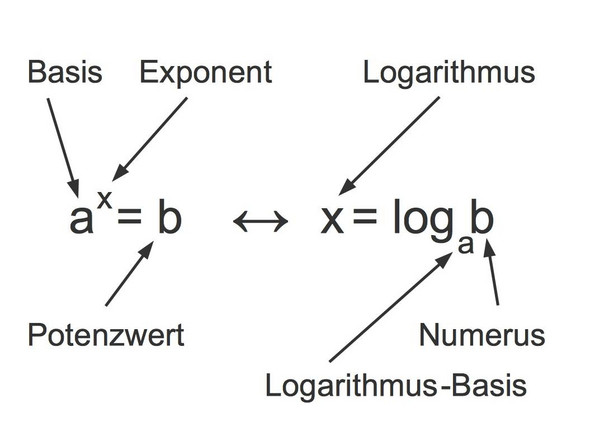
Das kommt auf die Basis ist. Ist keine Basis angegeben, so ist sie die 10.
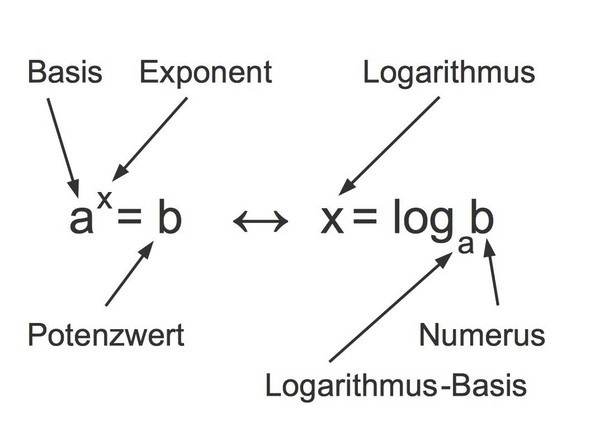
Mit dem Logarithmus kannst du den Exponenten errechnen. Heißt, du gibst in die Logarithmusklammer den Numerus ein und davor die Basis, und dann hast du den Exponenten.
Dein Beispiel ist log(30), also keine Basis angegeben, somit ist sie die 10. Wir haben:
10^x = 30
Mit dem Logarithmus erhältst du den Exponenten x, also ca. 1.47. Willst du das umkehren, nimmst du die Basis und als Exponenten den Exponenten. Also 10^1,47 = 30.
dann 10^1,47712125 = 29,9999999 = 30
und
7 - lg x = lg 847,4
lg x = 7 - lg 847,4
x = 10^(7-lg 847,4)
x = 11800
Im gleichen Atemzug, könnte mir vllt jemand bei der Lösung der Aufgabe 7-lgx=lg847.4 helfen also die einzelnen Arbeitsschritte