Lösungsmenge quadratische Ungleichung?
Hallo, wie würdet ihr die Lösungsmenge folgender quadratischen Gleichung x^2 - 34*x + 289 > 0 berechnen? Ich bin mit Betrag ( |x - 17| > 0) auf x > 17 und x < 17 gekommen. Wie lautet dann die Lösungsmenge?
4 Antworten
das ist doch die binomische Formel (x-17)²>0
Das Quadrat ist immer >=0. Es ist gleich 0 für x=17. also muss man 17 ausschließen
Die Ungleichung ist erfüllt für alle x Element R ohne 17
Wenn du für x 0 einsetzt, dann ist die Ungleichung auch erfüllt. Also ist deine Lösung falsch
(und wenn du für x 18 einsetzt ist sie auch erfüllt.)
Nein ist sie nicht, Null zählt auch dazu, oder willst du etwa behaupten, dass 0 nicht kleiner als 17 ist?
Mein Fehler; ich hatte irgendwie ein Minus (das nicht drin ist) reingelesen und gedacht deine Antwort wäre x<-17 oder x>17. Sorry
Nicht schlimm. Passiert mir auch manchmal...Haha
Hallo
Ich würde das ganze so lösen, dass ich daraus eine Gleichung mache ( > mit = ersetzen) und danach einfach nach x auflöse. Da ich bei der Wurzel immer + und - minus haben kann gäbe es zwei Lösungen, da aber beide das Gleiche ergeben, bedeutet dass, das es egal ist, ob die Zahl grösser oder kleiner als die Lösung ist um das > zu erfüllen, da ein < nie erfüllt werden kann. Und als Lösungsmenge würde ich einfach alle Reelen zahlen ausser 17 angeben.
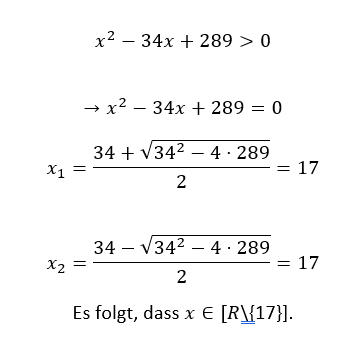

wie kommst du auf den Betrag?
Der Betrag ist immer >=0 für alle x
hast du die abc-Formel (oder pq-Formel) benutzt?
Quadratischer Ergänzung, dann Binomische Formel, dann Wurzel ziehen...
Du hast die Lösungsmenge bereits in deiner Antwort stehen!!!
Nämlich: "x > 17 und x < 17"
Wenn du das aber ausrechnest kommst du auf x<17 und x>17 und das geht viel schneller