Muss Lösungsmenge einer quadratischen Ungleichung bestimmen?
Hallo
Ich habe eine Frage zur folgenden Aufgabe:
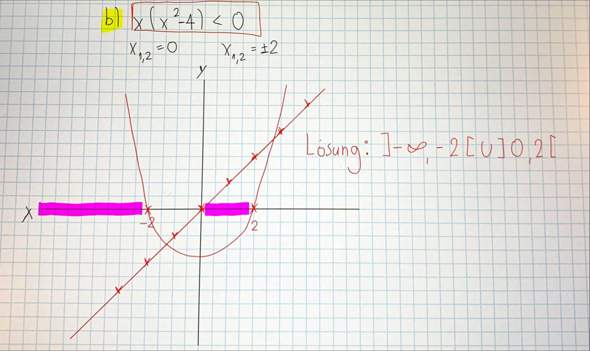
Was ich rot umrahmt habe ist die Ungleichung, von der die Lösungsmenge bestimmen werden muss. Ich habe selbst die Parabel und die lineare Funktion als Hilfe gezeichnet, stimmen sie ? . Was ich rot markiert habe sind die Lösungsmengen, ich verstehe nicht wie man darauf kommt ?
Ich meine die Lösungsmengen erfüllen nicht die Bedingung der Ungleichung?
Wäre dankbar für eine Erklärung
2 Antworten
Nullstellen x_1 = 0, x_2 = -2 und x_3 = 2 passen, ebenso die angegebene Lösungsmenge.
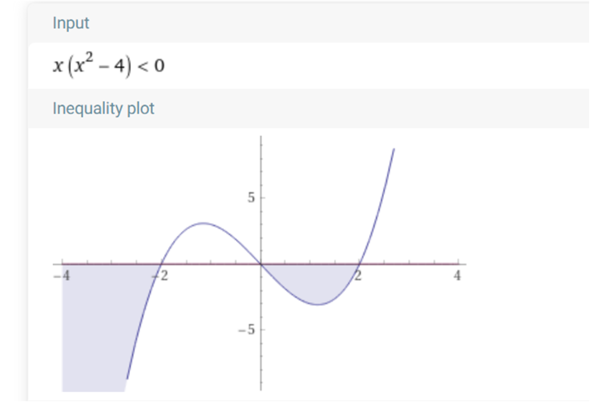
Um die entsprechenden Bereiche zu finden, kann man die Funktion f(x) = x * (x² - 4) skizzieren und die Nullstellen kennzeichnen. Die Bereiche, in denen die Funktionswerte unterhalb der x-Achse liegen, sind bei "kleiner als Null" gesucht.
man kann auch überlegen :
damit das Produkt negativ wird ( < 0 )
.
Fall 1
x < 0 , dann muss x²-4 positiv sein .
Das ist ab x = +2 ( x>2) oder x = -2 ( x < -2) der Fall.
Nur x < - 2 kommt in Frage, x>2 der Voraussetzung wider spricht
(-unend ; -2)
.
Fall 2
x > 0 , dann muss x²-4 negativ sein
Das Intervall ist -2 > x < +2 .
Passt nur mit dem Intervall ( 0 ; 2 ) zusammen .
:
Die RundenKlammern entsprechen den nach außen eckigen bei dir ( die auch richtig sind )
.
Was Gauss58 meinte
x*(x² - 4) = x³ -4x als Graph anzeigen lassen.
Reicht nicht als Lösung hilft aber bei der Kontrolle.
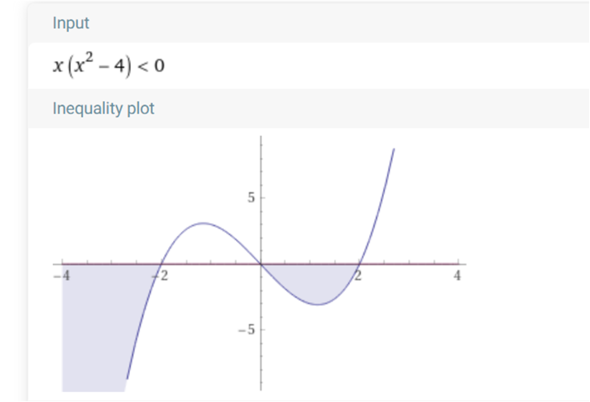
PS : deine beiden Graphen helfen leider nicht bei der Lösung, die Schnittpunkte liegen bei
-1.56 und 2.56