Lösung der Mathe-Aufgabe Trigonometrie?
Hey:)
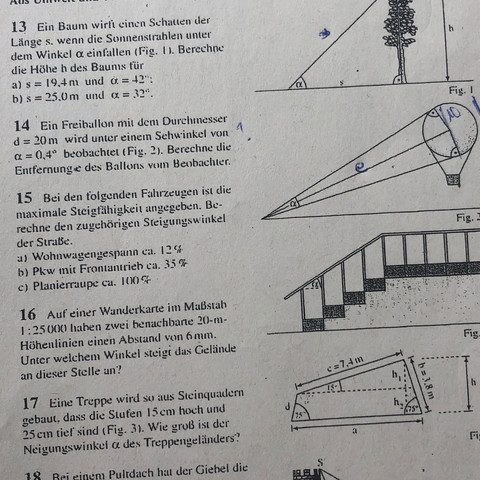
Gibt es eine Person, die mir helfen kann, wie man diese Aufgabe (Aufgabe 14 auf dem AB) berechnet.
Das Ergebnis ist angeblich e = 2865 Meter, aber ich verstehe nicht, wie man darauf kommt... ich hab 0.07 herausbekommen 😂
Also Danke für alle Mathe-Genies
3 Antworten
Verwende die Definition des Sinus und stelle nach e um. (Darauf achten, dass nur der halbe Winkel relevant ist …)
Entfernung (Hypothenuse im rechtwinkligen Dreieck) = 10 / sin(0,2°) = 2864,79 m.
Warum 0,2° ? Die Hälfte von 0,4° und 10 ist die Hälfte vom Durchmesser also Radius = 10 m.
LG,
Heni
Da Du aber nicht bis zum Mittelpunkt des Ballons sehen kannst, sondern nur bis zur Hülle, müßtest Du von dem Ergebnis noch 10 m, also den Radius des Ballons abziehen. Das Ergebnis wäre dann die Entfernung vom Auge bis zum Punkt auf der Hülle, der dem Auge am nächsten ist.
Außerdem solltest Du den Tangens nehmen. e ist eine Kathete, nicht die Hypotenuse.
Herzliche Grüße,
Willy
Allerdings ist geht e in der Skizze tatsächlich bis zum Mittelpunkt; dann sollte man das mit den 10 m bleiben lassen.
Außerdem sind Tangens und Sinus bei solch kleinen Winkeln praktisch identisch; ist also letztendlich wurscht, was man nimmt.
Alles in allem war mein Kommentar überflüssig, wenn ich so darüber nachdenke.
Hätte ich auch dazu tendiert, aber in der Figur ist e als Hypothenuse dargestellt und 2. macht es bei dieser Entfernung keinen Unterschied.
ich habe es eben auch nicht gerafft !
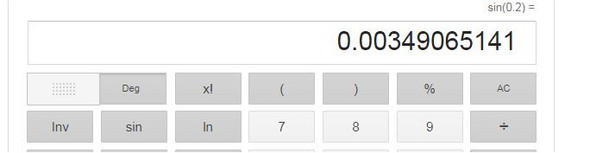
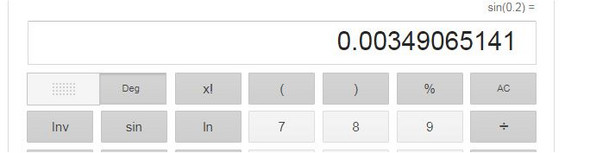
Man muß schauen ,daß Grad !! eingestellt ist
Dann ist sin (0.2°) = 0.00349 und man erhält die 2865 Meter.
Bei sin (0.2 ) erhält man 0.1968
also sin (0.2°) = 10 / e >>>>> sin (0.2°) * e = 10 >>>> e = 10 / sin
DEG ist an, nicht RAD
Vergiß es; e ist doch die Hypotenuse. Habe nicht richtig hingesehen.
Genau das habe ich gemacht aber da kam dann 0.03 oder sowas raus😩