Lineare Funktion -ganz wichtig-?
Hallo, ich brauche unbedingt Hilfe.
Könnt ihr mir bitte diesen 9 vorsagen wie/wo ich die ins Koordinatensystem einzeichnen soll.
- y=0,4x
- y=2,5x
- y=1/2x
- y=5,6x
- y=6/7x
- Y=-2/3x
- y=2x
- y=-3x
- y=-5/7x
Wäre echt nett
lg

2 Antworten
nutz die app geogebra und Guck dir YouTube Videos dazu an, ist ganz einfach :)
ich habe echt viele Videos schon angeschaut, und verstehe das Thema trotzdem nicht:( wir schreiben morgen schon einen Test.
Die Lehrerin war ca 3 Wochen nicht da und müssen trotzdem einen Test schreiben sie meinte „wir sollen es uns auch selber beibringen da das Thema leicht ist“. Leider verstehen es nur 2/3 Schüler aus der Klasse die auch die 9te wiederholt haben und das Thema vor einem Jahr hatten🥲
allgemeine Form einer Geraden:
y = mx + n
n ist der y-Achsenabschnitt, wo die Gerade die y-Achse schneidet.
m ist die Steigung.
Ich würde den y-Achsenabschnitt markieren und dort das Steigungsstrecke anzeichnen.
n ist bei dieser Aufgabe immer 0. D.h. alle Geraden verlaufen durch den Ursprung. Das ist da, wo sich die Achsen schneiden.

Nun zum Steigungsdreieck.
Gehe vom Ursprung einen Schritt nach rechts und dann so viel nach oben oder unten, wie es die Steigung dir "sagt".
Ist die Steigung positiv, geht man nach oben.
ist die Steigung negativ, geht man nach unten.

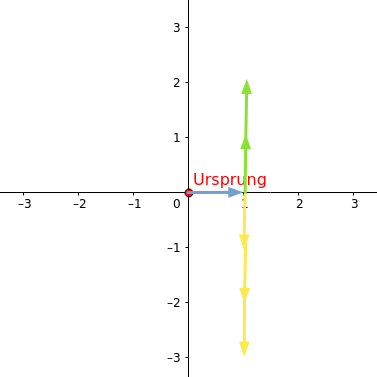
grüne Pfeile, Steigung m = +2
gelbe Pfeile, negative Steigung m = -3
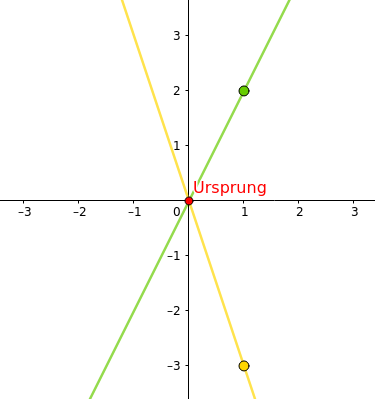
Das Ende der Pfeile markierst du wieder und zeichnest die Gerade durch den y-Achsenabschnitt und die durch die Steigung bestimmten Punkte:

Zahlen ohne Kommastellen kann man gut zeichnen. Bei Zahlen mit Nachkommastellen muss man sehr genau zeichnen. Die Steigung 2,5 oder 1/2 lässt sich noch ganz gut zeichnen, 6/7 eher nicht.
Ist die Steigung ein Bruch, kann man sie aber dennoch gut zeichnen.
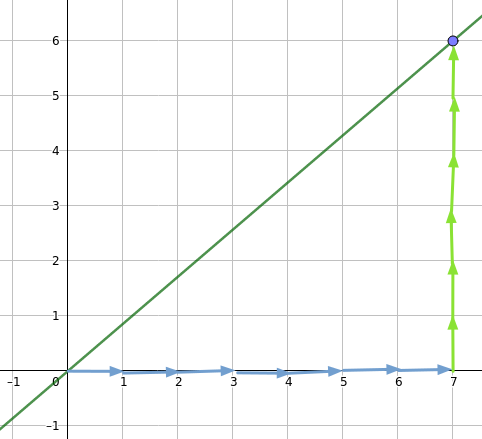
Den Nenner gehst du nach rechts (6/7) und den Zahler nach oben (positive Steigung) oder nach unten (negative Steigung), bei m = 6/7 also 6 nach oben:

Und man kann jede Zahl in einen Bruch verwandeln. Evtl. lohnt es sich, diesen Bruch zu kürzen.
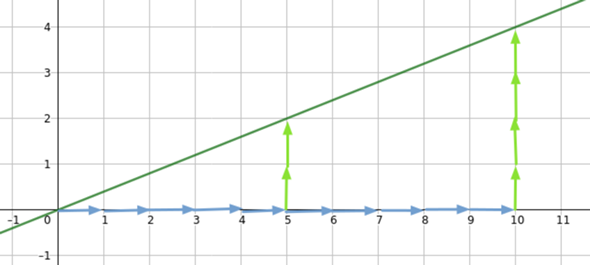
0,4 sind 4/10 oder 2/5
Also 5 nach rechts und 2 (2/5) nach oben oder 10 nach rechts und 4 (4/10) nach oben: