Liegt eine Funktion vor, wenn zu jedem x-Wert Höchstens ein Funktionswert zugeordnet ist?

Nein, das wäre dann eine Partielle Funktion. Für eine Funktion muss jedoch gelten, dass jedem x aus dem Definitionsbereich genau ein y aus dem Zielbereich zugeordnet wird.

Eigentlich zu jedem x-Wert genau ein Funktionswert.
x-Werte ohne Funktionswert müsste man aus der Definitionsmenge nehmen. Eine solche Definitionslücke wäre z.B. x=0 bei f(x)=1/x

und die Aussage “höchstens” impliziert ja einer oder keiner. Und “keiner” macht ein Problem!

also ganz sauber: Jedem x aus deer Definitionsmenge wird genau ein Funktionswert zugeordnet.

Eher eine Frage:

könnte man es nicht als Summe von Brüchen schreiben, bei denen an den x Stellen mit keinem Funktionswert der Nenner null wäre?

Bspw. f(x)=(1/x)+(1/x+1)+(1/x+1)

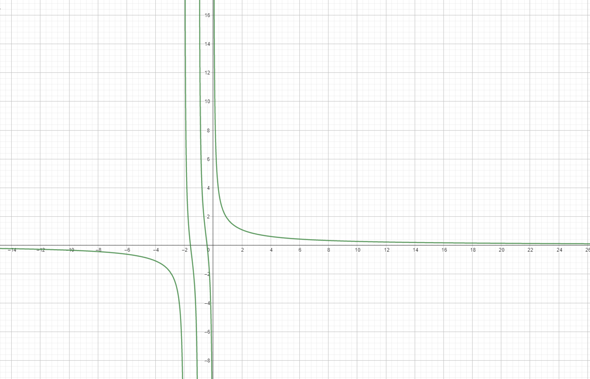
Bei dieser Funktion wird jedem Argument höchstens (manchmal keiner) ein Funktionswert zugeordnet, trotzdem ist es eine Funktion?!

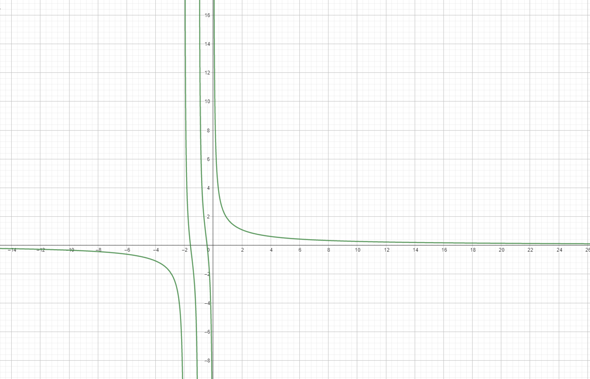
Nein, da bei einer Funktion jedem Argument (x-Wert) genau ein Funktionswert (y-Wert) zugeordnet werden muss. Bei höchstens einem kann ja auch einem Argument kein Funktionswert zugeordnet werden, was bei einer Funktion nicht funktioniert 😂

Sorry, kleiner Wortwitz 🙃🤣

Nein, nicht unbedingt.

"Höchstens ein Funktionswert" bedeutet, dass auch "kein Funktionswert" möglich sein kann.

Aber wenn einem x aus dem Definitionsbereich kein Funktionswert zugeordnet ist, dann ist's keine Funktion.