Kumulierte Wahrscheinlichkeit?

Kann mir jemand bei dieser Aufgabe helfen?

Answer 1

[TBDRM]

P(7 ≤ X ≤ 10) = {n=7, 10} nCr(20, n) p^n (1–p)^(20–n) = 0,53

Wenn du das ausrechnest, also

nCr(20, 7) p^7 (1–p)^13 + nCr(20, 8) p^8 (1–p)^12 + nCr(20, 9) p^9 (1–p)^11 + nCr(20, 10) p^10 (1–p)^10 = 0,53,

dann erkennst du, dass du insgesamt eine ganzrationale Funktion 20. Grades bzgl. p erhalten wirst. Definieren wir den Ausdruck oben als f(p).

Es gibt, da Grad(f) = 20, höchsten 20 Stellen pᵢ, sodass f(pᵢ) = 0,53 ist.

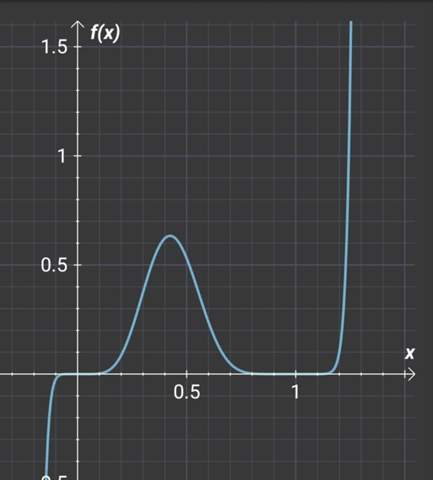
Dass es tatsächlich mehr als ein mögliches p gibt, kannst du mit dem Graphen begründen - er hat mit der waagerechten Geraden y=0,53 mindestns drei Schnittpunkte, mit p>0 (in der Grafik ist p=x).

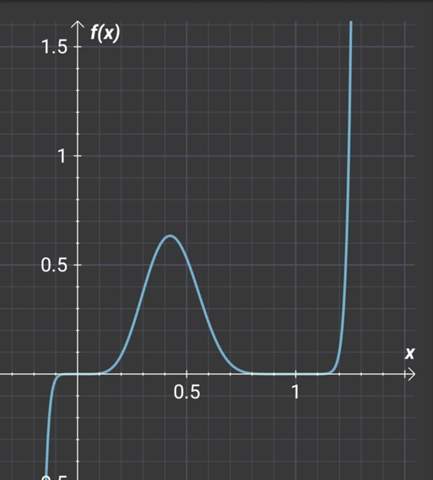
Um den ersten Aufgabenteil zu beantworten, können wir p ≈ 0,5 ablesen.

Woher ich das weiß: Hobby – Mathematik (u. Physik)