Kühlt sich Wasser bei kleinerer oder größerer Oberfläche schneller ab?
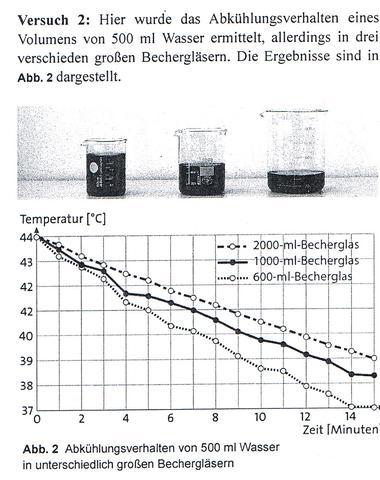
Im angefügten Bild ist eine Aufgabe. Dabei hat das Gefäß mit 600ml eine Oberfläche (des Wasser-Zylinders) von 381 cm², das mit 1000 ml von 397 cm² und das große mit 402 cm². Kann unter diesen Voraussetzungen die Grafik in der Aufgabe überhaupt richtig sein?
3 Antworten
Die Aufgabe ist ganz schön tricky, da sie der üblichen Faustformel vom Verhältnis Oberfläche zu Volumen widerspricht.
Dafür hätte ich 2 Erklärungen anzubieten:
Der Wärmeübergang (Wärmeverlust) ist nicht bei allen Flächen gleich. Da wäre z.B. der Boden, der nicht von kühlender Luft umströmt wird. Wenn der auf Holz oder einem anderen schlechten Wärmeleiter steht, geht da kaum Wärme verloren. Diese Fläche ist beim großen Glas am größten. Wie der Wärmeverlust an der Oberfläche im Vergleich zur Glaswand aussieht, kann ich spontan nicht sagen, könnte aber auch etwas geringer sein, als an der Seite, wo die Luft schön dran vorbeiströmen kann.
Eine Flüssigkeit, die umgerührt wird, kühlt schneller aus, als eine in Ruhe. In Ruhe muss die Wärme per Wärmeleitung von Innen nach Außen gelangen und Wasser ist doch kein sooo guter Leiter. Umrühren, sodass ständig neues warmes Wasser an die Außenwand gelangt, ist da wesentlich effektiver. Im großen Glas ist das Volumen sehr flach, da bilden sich kaum Wirbel, die wie umrühren wirken. Da ist das kleine Glas wesentlich besser für die Ausbildung einer freien Konvektion geeignet (vertikaler Wirbel: kaltes Wasser sinkt am Rand nach unten, warmes steigt in der Mitte auf).
In diesem Fall dürften diese beiden Effekt zum Messergebnis führen: beim großen Glas ist am meisten Fläche am Boden "isoliert", und zusätzlich bilden sich wesentlich schlechter Wirbel im Inneren durch die flache Form.
Tja, nun widerspricht obiger Versuch aber der Bergmannschen Regel und die Frage ist, warum?
Meine Betrachtung ist aus Sicht der Thermodynamik.
Die Abkühlung erfolgt auf Grund mehrerer physikalischer Prozesse:
- Wärmeleitung an die umgebende Luft, dabei gibts zwei Wege: Einmal an der oberen Oberfläche direkt an die Luft und zum zweiten indirekt über die Glaswand des Gefäßes
- Wärmestrahlung von allen Öberflächen an die Umgebung (thermische Strahlung)
- Durch Verdunstung von Wasser an der oberen Oberfläche (Verdunstungskälte)
Der dritte Effekt von diesen drei ist am größten und überwiegt betragsmäßig die beiden anderen bei weitem.
In dem ersten Gefäß (das mit 600ml) ist die Fläche, an der Wasser verdunsten kann, am kleinsten. In dem dritten Gefäß (das mit 2000ml) ist die Fläche, an der Wasser verdunsten kann, am größten.
Darum kühlt das Wasser in dem ersten Gefäß am langsamsten und in dem dritten Gefäß am schnellsten ab.
Die Grafik bestätigt das.
Korrektur: Die Grafik bestätigt das nicht - sondern das Gegenteil.
Dann diese Erklärung: In dem kleinsten Gefäß kann die mit Wasserdampf gesättigte Luft besser an die Umgebung wegströmen als in dem größten Gefäß.
Da es sich bei der Aufgabe um Biologie (Bergmannsche Regel) handelt, gehe ich inzwischen von einem grundlegenden Fehler in der Frage aus.
Ich hab mir diese Bergmannsche Regel mal angesehen. ich bin kein Biologe - aber was diese Regel besagt - glaub ich verstanden zu haben.
Wenn dieser Versuch diese Regel veranschaulichen soll - dann ist er meiner (physikalischen) Meinung nach denkbar schlecht geeignet dafür.
Bei der Regel geht es in erster Hinsicht um das Verhältnis von Volumen zur Oberfläche. Konkret um den Sachverhalt der "Skalierung" von physikalischen Effekten.
Der Versuchsaufbau liefert dazu keine sinnvoll verwertbaren Aussagen und und ist außerdem anfällig für "Seiteneffekte" - die das eigentliche Erkenntnisziel verfälschen können und sogar ins Gegenteil verkehren können. In diesem Fall der Effekt der Verdunstung.
Tiere, die in arktischen Breiten leben, regeln ihre Körpertemperatur nicht durch Schwitzen.
bei größerer kühlt es schneller
aber in relation zur masse wohl
die oberflächen kommen mir falsch vor
die unterschiede sind zu gering, bist du sicher, dass du die oberflächen richtig ausgerechnet hast?
Die Maße waren vorgegeben:600 ml h = 9 cm, r = 4,5 cm ; 1000 ml h=6,8 cm, r=5,25 cm; 2000 ml h = 4,0 r = 6,25 cm Die Formel für die Oberfläche ist A=2 x Pi x r x (h + r)
tatsache
ich denke aber, dass man nicht die gesammte oberfläche dafür nehmen kann
die oberfläche, die ans glas grenzt, wird anders abkühlen, als die an der luft
ja, aber wärme geht immer über die oberfläche
feuer auch, desshalb brennt ein baltt papier auch besser als ein geknülltes
Denkst Du, dass die Grafik in der Aufgabe einfach nichts mit den Zahlen zu tun hat?. Das sieht im Aufgabenblatt auch so zusammengeschnippelt aus.
Wieso? Der große Becher (mit der großen Oberfläche) ist nach 15 Minuten bei 39°C, während der kleine Becher (mit der kleinen Oberfläche) schon nach 9 Minuten (also schneller) dort angekommen ist. Ich hoffe, Du kannst mich noch vor dem Wahnsinn mit dieser Aufgabe retten ;-)
Die Frage bezieht sich auf die simple Betrachtung des Wassers, weil es um Biologie (Bergmannsche Regeln) geht. Das kann alles nur ein Fehler sein.