kreuzweise interpolieren
Hallo,
ich würde gerne wissen wie man kreuzweise interpoliert. Am liebsten ist mir eine Formel ;-)
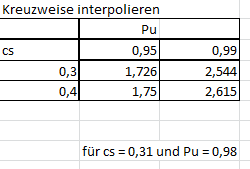
Ein Beispiel mit Werten hab ich als Bild beigefügt.
5 Antworten
A. Eine Gedanke zur Form der Formel für die lineare Interpolation, den ich ganz hilfreich finde, um die zu behalten:
s(x) = f(a) +(x -a) (f(b) - f(a)) / (b -a); x Element [a, b]
s ist eine Sekante der Funktion f durch die Punkte A(a|f(a), B(b|f(b). Die Formel zur linearen Interpolation entspricht daher einer Tangentengleichung, in der der Differenzialquotient ( = die Ableitung an der Stelle a) durch einen Differenzquotienten ersetzt ist, der die Steigung der Sekante durch A und B darstellt.
B. Ich denke mir in dein Bild ein Fadenkreuz mit einer Senkrechten durch Pu = 0,98 und einer Waagerechten durch sc = 0,31. Da schneiden sich die Strecken in der kreuzweise interpolierten Ordinate. Vielleicht deswegen...
psychironiker
Genau dafür gibt es das Geradengleichungs-Tool unter www.gerdlamprecht.de/Roemisch_JAVA.htm
Fall cs=0.3 und Pu ist bei mir x:
ergibt bei x-Input: 0.95 und 0.99 die lineare Gleichung:
y(x)=20.45 * x-17.7015
Fall cs=0.4
y(x)=21.625 * x-18.79375
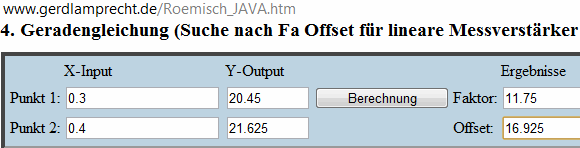
Nun baut man die Abhängigkeit der 4 Konstanten von cs in die Formel mit ein und benutzt
dabei das gleiche Geradengleichungstool wie oben siehe Bild:
Der Faktor sind also nicht mehr die 2 Werte 20.45 und 21.625, sondern die lineare Gleichung:
11.75 * cs+16.925
Der Offset sind also nicht mehr die 2 Werte -17.7015 und -18.79375, sondern die lineare Gleichung:
-10.9225*cs-14.42475
Beide Geraden in die obere Geradengleichung eingebaut ergibt eine Funktion in Abh. von x und cs:
y(x,cs)=( 11.75 * cs+16.925) * x -10.9225 * cs - 14.42475
Die Stützstelle einsetzen:
y(0.98,0.31)=2.34543
Ja, mathematisch wird einfach 3 bzw. 4 mal linear interpoliert. Die 2D-Ergebnisformel kann man übrigens schön in einem 3D-Diagramm als Fläche darstellen:
( 11.75 * y+16.925) * x -10.9225 * y - 14.42475
WARNUNG: Ich bin nicht vom Fach, meine aber trotzdem, dass aufgrund der Angaben recht klar ist, was an einer Interpolation nur "kreuzweise" sein kann:
A. Für Pu = 0,95 (Pu nenne ich mal Parameter) soll zwischen den angegebenen Werten 1,726 und 1,75 (nenne ich mal Ordinaten) für cs = 0,31 im cs-Intervall [0,3; 0,4] interpoliert werden.
Dann soll für Pu = 0,99 zwischen den Ordinaten 2,544 und und 2,615 ebenfalls für cs = 0,31 im cs-Intervall [0,3; 0,4] interpoliert werden.
"Kreuzweise" soll dann zwischen den beiden (je nach Parameter berechneten) interpolierten Ordinaten für den Parameter Pu = 0,98 im Parameter-Intervall [0,95; 0,99] interpoliert werden.
B. Ergebnisse: Erste interpolierte Ordinate 1,7248; zweite interpolierte Ordinate 2,5511, kreuzweise interpolierte Ordinate 2,345425
C. Kleines Q-Basic-Programm zur Ermittelung der Ergebnisse, das Elumanias Rechenbeispiel reproduziert; diesem ist die gewünschte Formel zu entnehmen (in drei Zeilen; zusammenbasteln ist formal möglich, ergibt aber ein eher unübersichtliches Ungetüm):
CLS
INPUT "Abszisse der unteren Grenzen der ersten Interpolation"; x0
INPUT "Ordinate der unteren Grenzen der ersten Interpolation"; f0
INPUT "Abszisse der oberen Grenzen der ersten Interpolation"; x1
INPUT "Ordinate der oberen Grenzen der ersten Interpolation"; f1
INPUT "Abszisse der ersten Interpolation"; x
f = (f1 ‑ f0) * (x ‑ x0) / (x1 ‑ x0) + f0
PRINT "Ordinate der ersten Interpolation"; f
INPUT "Ordinate der unteren Grenzen der zweiten Interpolation"; g0
INPUT "Ordinate der oberen Grenzen der zweiten Interpolation"; g1
g = (g1 ‑ g0) * (x ‑ x0) / (x1 ‑ x0) + g0
PRINT "Ordinate der zweiten Interpolation"; g
INPUT "unterer Parameter"; p0
INPUT "oberer Parameter"; p1
INPUT "interpolierter Parameter"; p
h = (g ‑ f) * (p ‑ p0) / (p1 ‑ p0) + f
PRINT "kreuzweise interpolierte Ordinate"; h
psychironiker
Zufall, habe ich heute erst gemacht:
Formel f(x) = f0 + (f1 - f0) * (x - x0) / (x1 - x0)
gesucht: Pu bei x = 0,35
f ( 0,35) = 1,75 + ( 1,726 - 1,75 ) * ( 0,35 - 0,3) / ( 0,4 - 0,3)
f ( 0,35 ) = 1,738
Ich nenn das übrigens linear interpolieren.
Hallo Elumania, ich bin der Meinung, dass du Pu nicht berücksichtigt hast.
Der gesuchte Wert liegt zwischen 0,3<cs<0,4 und 0,95<Pu<0,99. --> Es wird eine "doppelte Interpolation" gefordert.
Ich habe als x- Werte 0,3 und 0,4 gewähl. Interpolieren tue ich zwischen 1,726 und 1,75. Da 0,35 genau die Mitte ist, ist auch die Mitte zwischen 1,726 und 1,75 gesucht und die ist:
0,5 ( 1,726 +1,75 ) = 1,738 Stimmt also.
Zwischen was du genau interpolieren möchtest kann ich natürlich nicht wissen. Ich habe nur lineare Interpolation zwischen zwei Werten gelernt. "Doppelt" Interpolieren sagt mir nichts.
wenn man drei mal interpoliert kommt man auch auf das ergebnis (s. Bild)
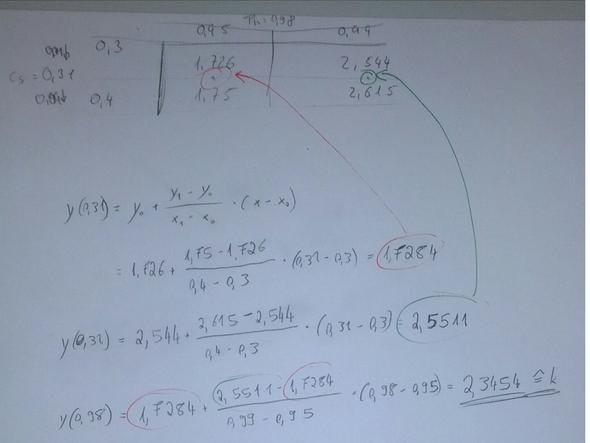
Da scheine ich richtig gelegen zu haben, was die Definition des Verfahrens angeht. Der Rest ist wohl eher eine Stilfrage.
psychironiker