Komplexe Zahlen,wie bestimmt man Real- und Imaginärteil?
Hallo, ich bin gerade in der Prüfungsphase und bin auf eine Sache gestoßen, die ich nicht nachvollziehen kann. Ich weiß was komplexe Zahlen sind. Auch wie ich die einfachen Sachen in Imaginär- und Realteil bestimmen kann... ZB z= 3+ (1/2)i . Die Eulersche Form und Trigonometrische Form sind für mich auch keine Fremdwörter.
ABER was ich als Datei hochgeladen habe kann ich nicht nachvollziehen. Angegeben ist es in eulerscher Form. Dann bei der ersten Zeile lässt man bei der "Umformung die 1 weg" (Warum?). Das ganze wird dann in die Trigonomialform umgewandelt....soweit komme ich noch mit..aber was danach passiert verstehe ich leider nicht :/
Ich wäre froh,wenn mir das jemand erklären könnte.
LG
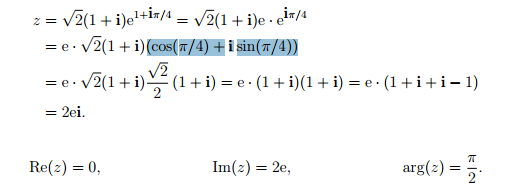
2 Antworten
Die 1 wurde nicht weggelassen, sondern das e^1 wurde als Faktor gemäß der Exponentialgesetze (wie in der Schule) abgesplittet:
e^(1+bla) = e * e^(bla)
Der nächste Schritt ist einfach nur die Polardarstellung der komplexen Zahl:
e^(i*bla) = cos(bla) + i*sin(bla)
Siehe auch: https://de.wikipedia.org/wiki/Komplexe_Zahl#Polarform
ok warum die 1 weg ist habe ich verstanden... . Das gilt:sin(π/4) = cos(π/4) = 1/√2 da hätte ich selber drauf kommen können :D aber dann habe ich doch da stehen: e*√2(1+i)*(1/√2+i*(1/√2))...ich verstehe aber noch nicht ganz wie ich dann auf -//- *(√2/2)*(1+i) komme... das ist doch (1+i)/√2 :(
Hallo,
wie Drainage bereits schrieb, wurde e^(1+i*π/4) gemäß dem Potenzgesetz
x^(a+b)=x^a*x^b in e^1*e^(i*π/4) umgewandelt.
Nach der sogenannten Eulerschen Identität ist e^(i*φ)=cos (φ)+i*sin (φ).
Nun mußt Du noch wissen, daß π/4 einem Winkel von 45° entspricht und daß bei diesem Winkel der Sinus und der Kosinus gleich sind, nämlich √2/2.
e^1=e; dies wurde als Faktor ganz nach vorn gezogen.
Nun nur noch alles einsetzen und zusammenfassen:
e*√2(1+i)*(cos (π/4)+i*sin (π/4))=
e*√2(1+i)*(√2/2+i*√2/2)
√2/2 wird ausgeklammert:
e*√2*(1+i)*√2/2*(1+i)
√2*√2/2=2/2=1
Es bleibt e*(1+i)*(1+i)=e*(1+2i+i²)
Da i²=-1, bleibt in der Klammer nur 2i übrig und e*2i=2*e*i
Herzliche Grüße,
Willy
Vielen Dank für die Antwort!!! Jetzt hat es klick gemacht :)
Danach setzt du einfach die Werte von sin und cos ein, falls dir das auch noch unklar sein sollte: sin(π/4) = cos(π/4) = 1/√2