Komplexe Zahl in kartesischer Darstellung und in der Polarform?
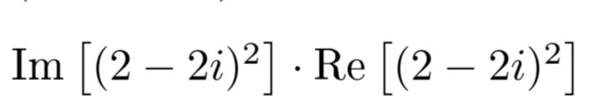
Wie kann ich folgenden Ausdruck in kartesischer Darstellung und in der Polarform angeben? Rein intuitiv würde ich sagen, da der imaginäre Teil von der linken komplexen Zahl eine - 2 ist und der Realteil der rechten Zahl eine zwei ist, dass es sich hier einfach um eine reelle Zahl handelt, wo ich die Gaußsche Zahleneben gar nicht heranziehen muss. Das wirft mich aus der Bahn. Welche Schritte muss ich also jetzt tätigen, um die Aufgabe zu lösen?
Vielen Dank im voraus!
1 Antwort
Einfach den inneren Term (der ja bei beiden Teilen gleich ist) umformen, so dass du dann den Real- bzw. Imaginärteil direkt ablesen kannst
(2 - 2i)^2 = 4 - 8i - 4 = -8i
Der Realteil davon ist 0, der Imaginärteil ist 8 => Das Ergebnis ist 0
Der Imaginärtiel ist natürlich -8, sorry Schreibfehler von mir oben
Ist der imaginäre Teil - 8 oder 8? Bin noch nicht so familiär mit den komplexen Zahlen