Komplexe Zahlen Satz von Moivre und Komplexe Zahlen?
Hallo,
Und zwar habe ich ein Problem zu erkennen wann ich Minus/Plus oder kein Pi rechne.
Habe ein Paar Screenshots von Aufgaben reingepackt. Der Rest der Aufgabe ist mir bewusst nur der eingekreiste Teil den konnte ich noch nicht erschließen. Gibt es eine einfache Methode wo ich erkennen kann ob ich jetzt Pi dazu machen muss oder nicht? Verstehe nämlich den Sinn davon leider nicht

2 Antworten
Du musst dir Überlegen, in welchem Quadranten die Zahl liegt!
Der arctan liefert nur Winkel von -pi/2 bis pi/2, also für den ersten und und vierten Quadranten.
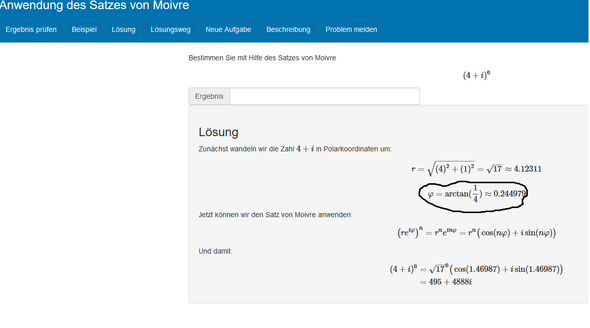
Deine erste Lösung liegt im ersten Quadranten (sowohl Realteil, als auch Imagiärteil sind positiv), daher brauchst du keine Korrektur:
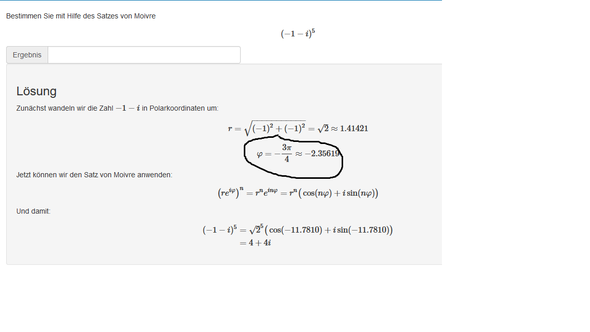
Deine zweite Lösung liegt im 2. Quadranten, da der Realteil negativ ist, der Imaginärteil positiv. Da der arctan hier einen wert im vierten Quadranten liefert, muss der wert korrigiert werden.
Bei deiner dritten Lösung wird der Winkel direkt angegeben, da man gleich sieht das dieser ein 45° Winkel nach links unten ist - hier hat man sich die Rechnung gespart.
Mein Tipp:
Zeichne zunächst die Punkte in der komplexen ebene ein, und dann dazu den Winkel, den du berechnst - dann siehst du sehr schnell, wann du warum welche Korrektur brauchst.
Dem ist nichts hinzuzufügen.
Als Ergänzung aus einem anderen Gebiet: in den üblichen "mathematischen Standardbibliotheken" in der Computer-Programmierung gibt es die Funktion arctan2(x,y), die statt einer einzigen Zahl zwei Zahlen annimmt, nämlich die Rechteckkoordinaten eines Punktes/Vektors. Damit übernimmt diese Funktion nicht nur die Prüfung, in welchem Quadranten man sich gerade befindet, sondern vermeidet auch die "Singularität" bei x = 0.
Das ist doch eigentlich gar nicht so schwer.
Du musst dir nur immer folgendes klarmachen. In welchem Quadranten desKOS liegt den der Pfeil? RE repräsentiert dabei den x-Wert, IM den y-Wert.
RE+ \ IM+ -> erster Quardrant
RE- \ IM+ -> 2. Q
RE- \ IM- -> 3. Q
RE+ \ IM- -> 4. Q
Im math. pos. Drehsinn hast du dann:
Im ersten Quadranten hast du Werte von 0° bis 90°, im zweiten 90° bis 180°, im dritten 180° bis 270° und im letzten dann 270° bis 360°
Im math. neg. Drehsinn hast du dann:
Im ersten Quadranten wieder 0-90°, im vierten -0° bis -90°, im dritten -90° bis -180°, im zweiten -180° bis -270° und dann bist du wieder im ersten. Für dessen Werte 0° bis 90° kannst du aber auch -270° bis -360° annehmen.
Und damit kannst du deine Aufgaben lösen. Musst halt pro Quadrant 90° dazurechnen bzw abziehen, je nachdem wie rum du gehst.