KGV bestimmen mit Variablen?
Hab die Frage meinem Lehrer gestellt, deswegen sende ich einfach einen Screenshot davon.
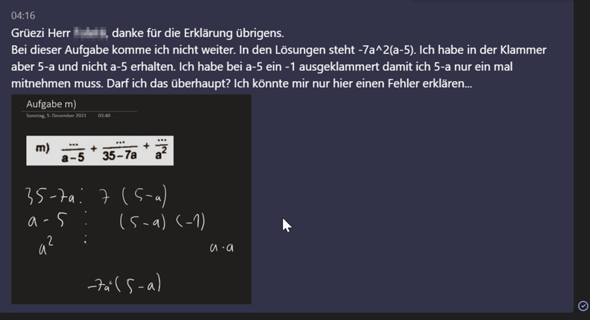
4 Antworten
Beides ist richtig. Du hast richtig gesehen:
und daraus den Hauptnenner (-1)(5-a) * 7 * a² = -7a²(5-a) gebildet.
Man kann aber genauso rechnen:
Und dann bekommt man als Hauptnenner (a-5)*(-7)*a² = -7a² (a-5). Du musst das dann nur beim Erweitern richtig machen:
Mit deinem Hauptnenner:
Mit der Lösung:
Am Ende kommt natürlich das Gleiche heraus, man muss nur jedes Mal bei jedem Bruch schauen, womit man ihn erweitern muss.
Letztendlich ist das das gleiche. Die kgVs unterscheiden sich nur durch den Faktor -1. Nach dem Erweitern und "Entfernen" des Hauptnenners unterscheiden sich die Gleichungen nur durch diesen Faktor -1, d. h. die Lösungsmenge ist dieselbe!
"Beweis":
Ich nehme als Zähler mal allgemein b,c und d:
b/(a-5)+c/(7(5-a))=d/a²
<=> (I) b/(a-5)+c/(-7(a-5))=d/a²
<=> (II) b/-(5-a)+c/(7(5-a))=d/a²
HN -7a²(a-5) => (nur Zähler) in (I) erweitert:
(III) -7a²b+a²c=-7(a-5)d
HN -7a²(5-a) => mit (II) erweitert:
(IV) 7a²b-a²c=-7(5-a)d
(III) = -1 * (IV)
Das kgV der ersten beiden Nenner ist
-7 (a-5)
Da a² nicht in das Schema passt, musst du es
wohl oder übel "dazumultiplizieren". Dadurch
entsteht
-7 a² (a-5)
Ja klar. Darum geht es ja - es gibt zwei Möglichkeiten, diesen Hauptnenner zu bestimmen, die sich eben durch das Vorzeichen unterscheiden. BEIDE sind richtig. Man muss das dann nur beim Erweitern richtig machen.
hast alles richtig gemacht!
Aber.... genauso könnte man doch auch sagen, dass ein KgV der beiden ersten Nenner (-1) * (7 *(5-a)) ist? Das ist doch nur eine andere Faktorisierung. Ob ich nun beim ersten Bruch die -1 heraus ziehe und beim zweiten eine 7 oder umgekehrt beim ersten nichts herausziehe, dafür aber beim zweiten eine -7, welchen Unterschied macht das?