Kann mir jemand helfen bei dem kürzen folgender Formel?
Ich verstehe das man einen der beiden (8x+1) mit dem Nenner kürzen kann. Wenn man aber beide wegkürzt müsste der Exponent des Nenners doch -2 betragen oder? Das ist die Musterlösung einer Ableitung.. kann mir jemand auf die Sprünge helfen?
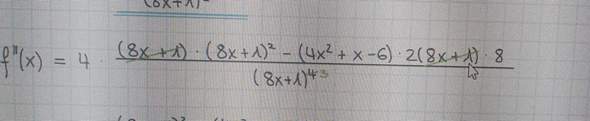
2 Antworten
Nein, kürzen darfst Du aus einer Summe eh nur, wenn das zu Kürzende in allen Summanden vorkommt!
Ausführlich notiert kannst Du zuerst im Zähler (8x+1) ausklammern; danach kürzt Du im Zähler nur noch "einmal" die Klammer mit der im Nenner...
Es gibt einen Spruch "aus Summen kürzen nur die Dummen", weil es oft falsch gemacht wird, bzw. man das zu kürzende nur aus einem Teil der Summe kürzt und nicht, wie nötig, aus ALLEN Summanden. Daher wird "empfohlen", zuerst auszuklammern und dann zu kürzen...
Ich mache es mal mit einfachen Termen:
(2x-7x²)/x³
Hier kommt in beiden Summanden des Zählers der Faktor x vor, d. h. man kann dieses x ausklammern und erhält:
x(2-7x)/x³. Jetzt kann man "gefahrlos" in Zähler und Nenner einmal den Faktor x kürzen, ergibt (2-7x)/x², d. h. im Nenner "verschwindet" nur ein x, nicht 2
"Könner" können auch ohne auszklammern direkt aus allen Summanden kürzen, aber natürlich dann hier im Nenner nur einmal, nicht zweimal...
Eventuell ein etwas aussagekräftigeres Beispiel:
(3x-x²)/(x^5+x^4+x³)
hier kann man wieder einmal das x aus allen Summanden kürzen, ergibt:
(3-x)/(x^4+x³+x²)
man kürzt nicht !!!! einen der beiden
oben steht eine Summe ( Getrennt durch das MINUS in der Mitte ) . Was man kürzt muss als Faktor in jedem Summanden vorhanden sein
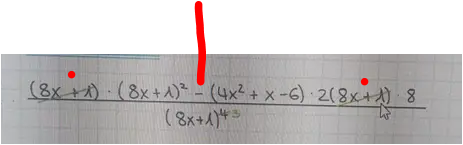
und verschwindet zusammen .
man könnte auch ( ohne Sinn allerdings ) mit (8x+1)³ kürzen . Dann bliebe vorne nur noch eine 1 und hinten müsste man 1/(8x+1)² hinschreiben
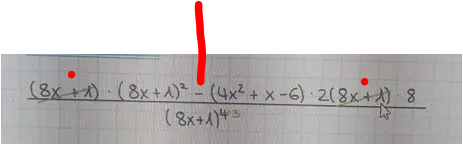
Heißt also dass das ganze falsch ist und so nicht gemacht werden darf? Es ist wie gesagt Teil einer Musterlösung....
irgendwie hab ich die Antwort nicht ganz verstanden