Kann mir jemand bitte helfen ich weiß nicht wie ich das begründen soll?
Ich weiß zwar welcher Graph zu welcher Funktion gehört dank einer App ich kann es nicht begründen
4 Antworten
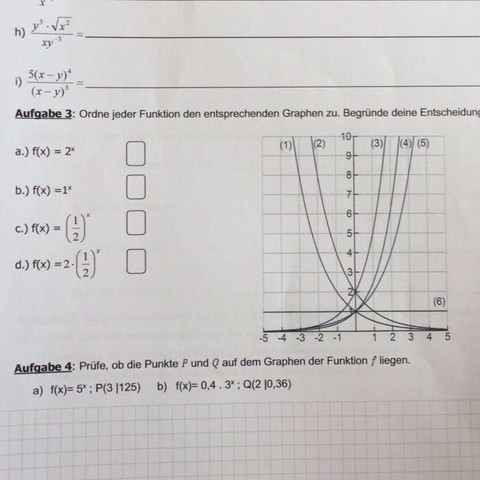
das sind alles Exponentialfunktionen, d. h. x ist im Exponenten.
Ist die Basis =1 ist das Ergebnis 1^x auch immer 1, also hast Du f(x)=1; ist sofort zu erkennen (Parallele zur x-Achse)
Ist die Basis kleiner 1, fällt der Graph nach rechts ab (Du multiplizierst ja eine Zahl mit sich selbst, die kleiner als eins ist, d. h. je öfter Du das machst (je größer x wird) desto kleiner wird die Zahl. Welcher Graph es letztendlich ist, findest Du am einfachsten raus, wenn Du für x z. B. den Wert 0 einsetzt und y ausrechnest.
Ist die Basis größer 1 steigt der Graph nach rechts immer weiter an. Auch hier mußt Du einen (oder zwei) Wert für x einsetzen um zu sehen, welcher Graph es letztendlich ist.
Das ist in diesem Fall besonders einfach, wenn du die Funktion für x=0 und x=1 ausrechnest (geht alles im Kopf) und nachguckst, bei welcher Funktion die y-Werte zutreffen. Statt x=1 kannst du auch x=2 nehmen, obwohl es bei einer schon fast aus dem Bild herausführt.
Das ist zwar eine simple Begründung, aber es ist eine.
1^x ist eine Konstante, denn egal was du für x einsetzt, es kommt 1 raus.
2^x ist stetig steigend. Graph 3 fällt raus, da der y-Achsenabschnitt nicht stimmt. Es kommen Graph 4 und 5 in Frage. Wir setzen 1 anstatt von x ein und sehen, dass Graph 5 der richtige ist.
(1/2)^x ist fallend und läuft gegen 0, das selbe gilt für 2*(1/2)^x. Es kommen die Graphen 1 und 2 in Frage. Aufgrund des Faktors 2 bei 2*(1/2)^x ist logisch, dass dieser Graph für jeden x-Wert höher liegt als der von (1/2)^x.
Es ist also naheliegend, welcher Graph hierbei zu welcher Funktion gehört.
Dann mach es doch rechnerisch.
Graph 3 kann für 2^x nicht stimmen.
Beim x-Wert 0 hat der Graph 3 den y-Wert 2.
2^0 ist aber 1, nicht 2.
Beim x-Wert 1 hat der Graph 3 den y-Wert 5.
2^1 ist aber 2, nicht 5.
Beim x-Wert 2 hat der Graph 3 einen hohen y-Wert.
2^2 ist aber 4, also nicht sonderlich hoch.
Auch Apps irren sich, deshalb halte ich von denen auch nicht viel. Mit selber denken kommt man viel weiter.
Für jeden schritt wird der wert immer mit der Basis multipliziert
Vielen Dank für deine ausführliche und aufwandreiche Antwort ich habe mithilfe der App funktionsplotter herausgefunden dass Graph 1,2,3und 6 infrage kommen :/ bist du dir da sicher ich kann solche Sachen nur rechnerisch beweisen aber nicht einfach erläutern ohne ne Rechnung