Ist eine stetige Funktion differenzierbar?
Weiß nämlich nicht was stetig heißt und Daniel Jung hats diesmal auch nicht gut erklärt.
3 Antworten
Stetig heißt salopp, dass die Funktion nicht springt und keine "Löcher" hat. Die Stetigkeit in einem Bereich ist eine notwendige, aber keine hinreichende Bedingung für Differenzierbarkeit.
Eine Funktion ist differenzierbar, wenn sie - wieder vereinfacht gesagt - keine "Ecken" hat.
Die Funktion Betrag(x) ist zum Beispiel stetig, aber im Punkt 0 nicht differenzierbar. (Die Steigung links von 0 ist konstant -1, rechts von 0 konstant +1. In 0 differieren linksseitiger und rechtsseitiger Grenzwert, hier kann also keine Steigung angegeben werden)
ok danke also ist diff. hinreichend für stetig und stetig notwendig für dif danke!
Jede differenzierbare Funktion ist stetig.
Aber nicht jede stetige Funktion ist differenzierbar!
Das ganze findest du genauso auch auf dem Bild:
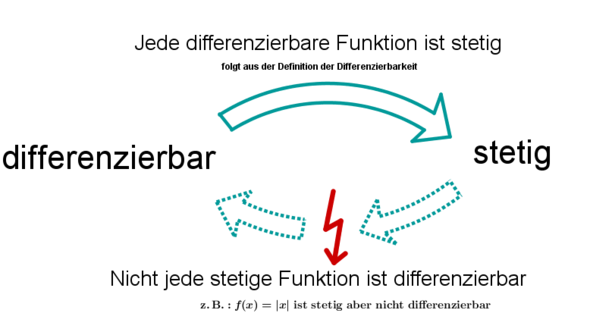
Hier findest du ausführliche Erklärungen dazu und auch beide Begriffe im Vergleich:

Stetig heißt auf Schulniveau, dass du die Funktion ohne den Stift abzusetzen in einem Stück zeichnen kannst. Polynome (x^2, Geraden), Sinus- und Kosinus, Wurzelfunktionen, e-Funktionen etc. sind alle stetig.
Gebrochenrationale Funktionen (1/x z.B.) sind dagegen nicht stetig, denn diese kannst du nicht an einem Stück zeichnen.
Klassisches Beispiel für eine stetige, aber nicht differenzierbare Funktion ist die Betragsfunktion. Denn differenzierbar heißt ja, dass du eindeutig an jedem Punkt eine Tangente anlegen kannst. Aber bei x=0 ist nicht klar, ob diese Steigung -1 (wie davor) oder 1 (wie danach) haben müsste. Deshalb ist die Funktion zwar stetig, aber in x=0 nicht differenzierbar.
Das ist falsch. Die gebrochenrationale Funktion f mit Funktionsgleichung f(x) = 1/x mit Definitionsbereich R\{0} ist stetig. Genauso jede andere gebrochenrationale Funktion.