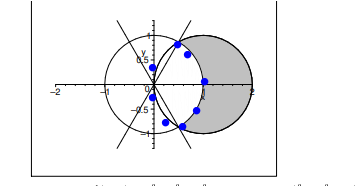
Integral mit Polarkoordinaten von zwei Kreisen?
Ich verstehe nicht ganz welchen Bereich wir hier genau suchen. Markiert ist der rechte Kreis, aber in der Menge steht ein "und" hätte deswegen gedacht wir müssen die Schnittmenge der beiden Kreise berechnen. Wie kommt man auf dem Bereich -pi/3 und pi/3 für phi? Müsste man nicht tan((sqrt(3)/2)/0.5) rechnen um phi rauszubekommen? Und warum wird dann die Polarkoordinatendarstellung der rechten Kreislinie berechnet aber dann nicht diese Grenzen für phi benutzt? Danke für die Antwort


2 Antworten
Wenn vor dem und ein ≤ 1 wäre, wäre die gesuchte Menge die Schnittmenge beider Kreise. Weil da aber ein ≥ 1 steht, ist die gesuchte Menge die Schnittmenge von außerhalb des Kreises einschließlich der Kreislinie mit dem rechten Kreis. Also passt die Zeichnung.
Die Schnittpunkte der beiden Kreise sind bei x = 0,5. Die Radien der Kreise sind 1. Es ist cos(π/3) = 0,5/1. Mit dem Tangens käme man auch auf den Winkel. Die y-Koordinate müsste man aber erst ausrechnen. Der Cosinus ist direkter.
Egänzung:
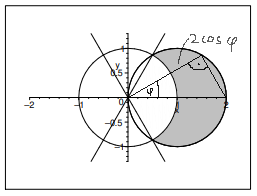
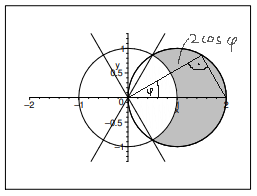
Gesucht ist die graue Fläche. Die Kreislinie des rechten Kreises lässt sich mit der Funktion r = 2 cos(φ) beschreiben. Der rechte Kreis stellt nämlich einen Thaleskreis dar. Das rechtwinklige Dreieck in diesem Kreis hat Hypothenusenlänge 2 und r ist die Ankathete zum Winkel φ. r ist deshalb 2 cos(φ). Jedoch liegt nicht die gesamte Ankathete in dem grauen Bereich. Die Länge 1 liegt immer im linken Kreis. Darum wird im inneren Integral von 1 bis 2 cos(φ) integriert. Außen wird von -φ/3 bis φ/3 integriert, denn das ist der Bereich, in dem die graue Fläche liegt und man die Länge des in der grauen Fläche liegenden Teiles der Ankathete als 2cos(φ) - 1 darstellen kann.
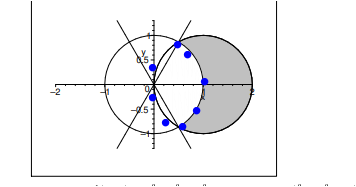
der Bereich ist NICHT >= 1