Cosinus in Pi umrechnen?
Woher weiß man dass cosphi = -sqrt(2)/2 bedeutet dass phi=3pi/4 ist?
(ich meine, cos^-1 von -sqrt(2)/2 kann ich in den TR eingeben, kommt 135 raus (aber warum bei DEG... dachte bei RAD))
3 Antworten
Das weiss man nicht "einfach". Erst wenn man's gelernt hat. So wie man Zahlenreihen lernt. "Ist einfach so" ist halt auch ausnahmsweise eine richtige Antwort.
- ein Kreisumgang ist entweder 360 Grad (DEG am Taschenrechner), oder eben 2Pi (RAD am Taschenrechner). Das ist halt das Verhältnis von Bogenlänge zu Radius
- Ein paar charakteristische Werte ergeben sich aus dem Pythagoras:
- Quadrat mit Diagonale: 45 Grad Winkel; Diagonale ist Seite mal Wurzel(2)
- Gleichseitiges Dreieck (60 Grad Winkel): Die Höhe im Dreieck hat die Länge von [Wurzel(3) ] / 2; der halbe Winkel ist 30 Grad, das Verhältnis der halben Seite zur ganzen Seite logischerweise 0,5 ; und das ist der Sinus von 30 Grad.
Vielleicht hilft dir das:
Ist doch kein Problem, wenn Pi = 180 Grad ist, dann ist 3 * Pi / 4 = 135 Grad.
ja und woher hat man 3 * Pi / 4 errechnet? ja wohl kaum im kopf
Hast dir viel Arbeit gemacht, hoffentlich fällt das auf fruchtbaren Boden...
Ja, hoffentlich hilft's. Aber einen Versuch ist es Wert.
okay vielen dank aber woher weißt du dass zB sin(30 Grad) = 1/2 * sqrt(1) ist?
Das ist ein billiger Trick, um sich den Sinus der wichtigsten Winkel einzuprägen. Daraus kann man sich nämlich auch deren Cosinus und Tangens ausrechnen.
achso ehrlich? sin(... Grad) = 1/2 * sqrt(...) ist sone art standardformel die die meisten wohl schon im Abi gelernt haben?
Es gibt, ehrlich gesagt, keine Erklärung dafür. Es ist eben (mehr oder wenig zufällig) so. Diese Eselsbrücke kann aber hilfreich sein.
moment mal, sind das echt diese unregelmäßigen 30er/15er-schritte? irritiert mich grad bisschen...
Ja, es gibt keine vernünftige Erklärung dafür, es ist eben so. Aber es ist eben eine gute Merkhilfe.
DEG für Grad zahlen
RAD für Bogenmaß (Teile von Pi)
Bei dieser Frage habe ich mich lebhaft an eine Prüfungsklausur mit einer Aufgabe mit Schmitz-Karte (Smithchart) erinnert.
Für die Berechnung hatte ich einen Ti Taschenrechner, nachdem mir mein HP64 gestohlen worden ist. Durch Verwechselung von Grad und Bogenmaß kam ich auf einen Wert Kapazitiv, der Induktiv hätte sein müssen. Das habe ich vermerkt und volle ! Punktzahl bekommen.
Danke für die höchst amüsante Erinnerung.
Na gut, dann müssen wir weiter ausholen.
wir haben (Vorzeichen erstmal weglassen) 1/2 * sqrt(2). Interessante Winkel sind 0, 30, 45 60 und 90 Grad. Es gilt
sin(0 Grad) = 1/2 * sqrt(0)
sin(30 Grad) = 1/2 * sqrt(1)
sin(45 Grad) = 1/2 * sqrt(2)
sin(60 Grad) = 1/2 * sqrt(3)
sin(90 Grad) = 1/2 * sqrt(4)
Jetzt suchen wir einen Winkel, dessen Sinus = 1/2*sqrt(2) ist und finden 45 Grad.
Da aber der Cosinus gegeben ist, ist der gesuchte Winkel 90 Grad - 45 Grad = 45 Grad. (ist in diesem Fall egal)
Jetzt gucken wir uns das Vorzeichen an. Da der Cosinus negativ ist, liegt der Winkel im zweiten (oder auch im dreitten) Quadranten:
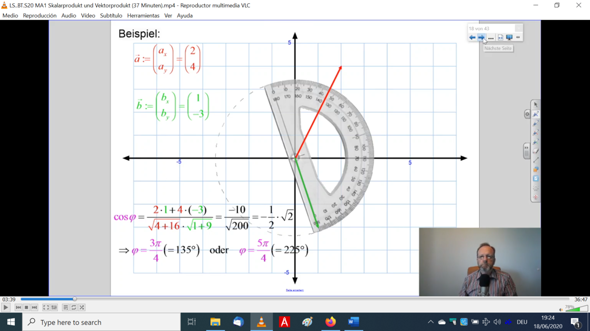
Gesuchter Winkel = 180 Grad - 45 Grad = 135 Grad. Auf der Zeichnung kann man das schön sehen.