Höhe einer Pyramide berechnen mit nur der Mantelfläche und der Kante "a"?
Wie kann ich die höhe einer fünfseitigen Pyramide mit der Mantelfläche berechnen?
.
Und mit der Kante "a"
3 Antworten
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Mathematik, Geometrie
Die Höhe könnte man wie folgt berechnen. Nachfolgend ein Beispiel.
hs = M * 2 / a / 5
hs = 7058,8745 * 2 / 40 / 5
hs = 70,588745
ha = (a/2) / tan(γ)
ha = (40/2) / tan(36)
ha = 27,52763841
h = Wurzel(hs² - ha²)
h = Wurzel(70,588745^2 - 27,52763841^2)
h = 65
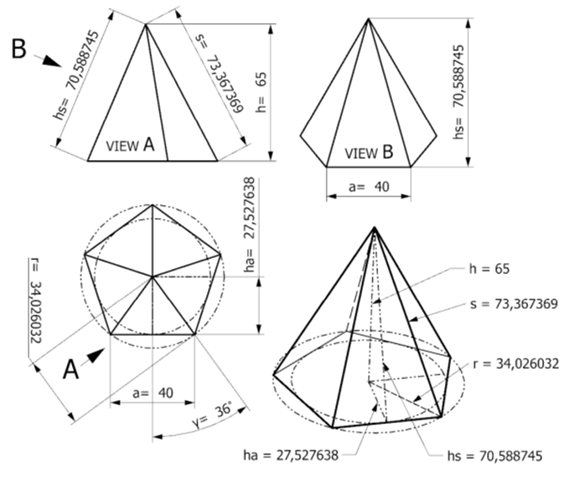
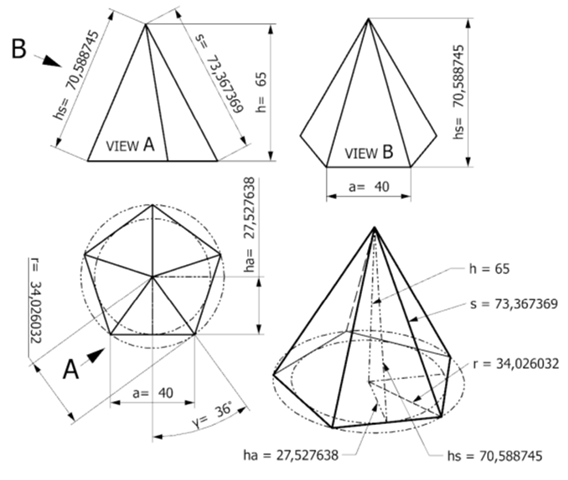
Das ist möglich. Ich würde spontan die Manteldreiecke betrachten und das Fünfeck in fünf Dreiecke zerlegen. Dann sollte man mit dem Pythagoras die Höhe in Abhängigkeit von Am und a herausbekommen.
Nur mit der Mantelfläche kann man die Höhe nicht berechnen.
Die Kante a ist noch gegeben das habe ich vergessen zu erwähnen sry