Graph der Ableitungsfunktion zeichnen?
Hallo,
ich bin leider unschlüssig wie diese Aufgabe zu lösen ist. Könntet ihr mir Lösungshinweise geben, sodass ich den Graphen gezeichnet bekomme?

1 Antwort
Hinweise:
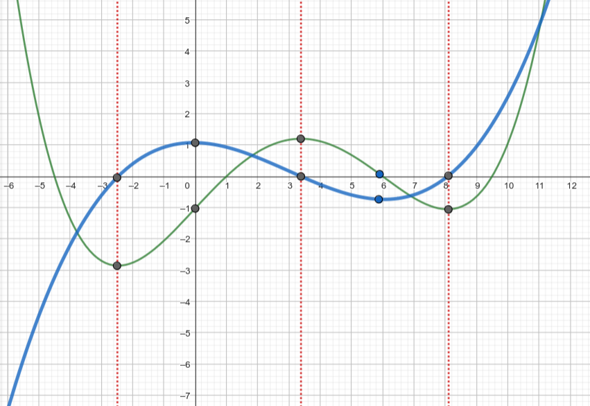
- Die Steigung wird für x gegen -∞ immer steiler negativ und daher verschwindet die Ableitungsfunktion auch gegen -∞ für x gegen -∞
- Die Steigung wird für x gegen +∞ immer steiler positiv und daher verschwindet die Ableitungsfunktion auch gegen +∞ für x gegen +∞
- Die gegebene Funktion hat 3 Extremwerte und genau an diesen Stellen hat dann die Ableitung eine Nullstelle (x ≈ -2,5; x ≈ +3,5; x ≈ +8)
- Bei etwa x = 0 befindet sich ein Wendepunkt mit der Steigung von ca. 1 und damit ist der Funktionswert der Ableitung etwa 1 und das ist gleichzeitig einen Extremwert der Ableitungsfunktion (Über den Wechsef der Krümmung "gegen den Uhrzeigersinn" nach "im Uhrzeigersinn" kannst Du erkennen, dass es ein Maximum der Ableitungsfunktion sein muss)
- Ein weiterer Wendenpunkt befindet sich etwa bei x=5,5 mit der Steigung von grob - 1 und damit hast Du einen weiteren Extremwert der Ableitung (Über Krümmung von "im Uhrzeigersinn" nach "gegen Uhrzeigersinn" kannst Du erkennen, dass es ein Minimum der Ableitungsfunktion sein muss)
- Wenn man Spaß dran hat, kann man noch ein paar Tagenten an den gegebenen Graphen malen und mithilfe eines Steigungsdreiecks ein paar Funktionswerte der Ableitungsfunktion bestimmen
Insgesamt komme ich dann zu etwa folgenden Bild (der blaue Graph ist der Graph der Ableitungsfunktion)