Flächeninhalt von einem prisma berechnen?
Hallo Leute,
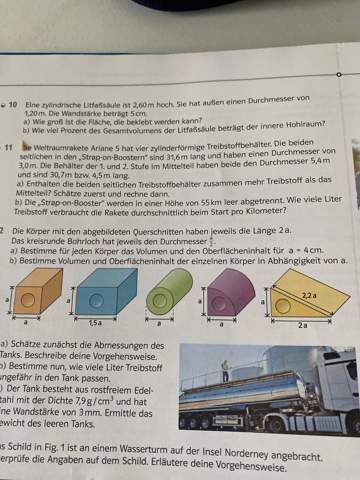
und zwar wollte ich fragen ob ihr meine Aufgaben korrigieren könntet ,zu der Aufgabe 12a&b die letzte Figur ,danke im Voraus!
1 Antwort
Ich komm bei den Dreieckprisma auf folgende Ergebnisse.
Aufgabe 2.5a
Dreieckprisma 1 Fläche A
A = 2a * a / 2
A = 8 * 4 / 2
A = 16 cm²
---
Dreieckprisma Volumen ohne Bohrung V
V = (2a * a / 2) * 2a
V = A * h
V = 16 * 8
V = 128 cm³
---
Fläche Bohrung A2
A2 = 0,25a^2 * pi
A2 = r² * pi
A2 = 1^2 * pi()
A2 = 3,141593 cm²
---
Bohrung Volumen V2
V2 = (0,25a^2 * pi * 2a) * 2a
V2 = A2 * h
V2 = 3,141593 * 8
V2 = 25,132744 cm³
---
Volumen gesamt Vg (mit Bohrung)
Vg = ((2a * a / 2) * 2a) - ((0,25a^2) * pi * 2a)
Vg = V - V2
Vg = 128 - 25,132744
Vg = 102,867256 cm³
---
Oberfläche ohne Bohrung O1
O1 = ((2a * a / 2) * 2) + ((2a + a + 2,2a) * 2a)
O1 = 2G + M
O1 = ((8 * 4 / 2) * 2) + ((8 + 4 + 8,8) * 8)
O1 = 198,4 cm²
---
Oberfläche Gesamtkörper mit Bohrung Og
O = (2a * a) + ((2a + a + 2,2a) * 2a) - (0,25a^2 * pi * 2) + (0,25a * 2 * pi * 2a)
Og = O1 - (2 * A2) + ( (0,25 * a) * 2 * pi() * (2 * a) )
Og = 198,4 - (2 * 3,141593) + ( (0,25 * 4) * 2 * pi() * (4 * 2) )
Og = 242,3822964574 cm²
------------
Aufgabe 2.5b
V = ((2a * a / 2) * 2a) - ((0,25a^2) * pi * 2a)
V = (a³ * 2) - (0,125 * a³ * pi) )
V = (2 * a³) - (0,3926990817 * a³)
---
O = (2a * a) + ((2a + a + 2,2a) * 2a) - (0,25a^2 * pi * 2) + (0,25a * 2 * pi * 2a)
O = (2 * a²) + (10,4 * a²) + (2,74889357 * a²)
Eigentlich müßtest du bei deinen Formeln nur die Zahlen einfügen.
Aber klappt irgendwie nicht mit den Formeln. Vorschlag: Nimm Folgende.
Die sind auch etwas einfacher.
V = ((2a * a / 2) * 2a) - ((0,25a^2) * pi * 2a)
O = (2a * a) + ((2a + a + 2,2a) * 2a) - (0,25a^2 * pi * 2)
kannst du noch die Lösungen von 12b schreiben
Ich hab mal meinen obigen Beitrag ergänzt mit Aufgabe 2.5b
Ich meine z.b 2a *a sind =a^2 oder so checkst du?
Ach so zurückkürzen. Ich hab mal meinen Beitrag oben ergänzt. Mit zurückgekürzten Formel. Mehr ist mir jetzt nicht eingefallen.
Ich hab meinen Lehrer heute gefragt und er meinte das die Rechnung falsch ist
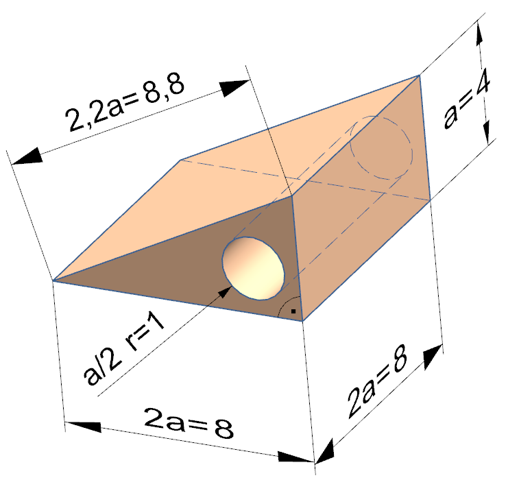
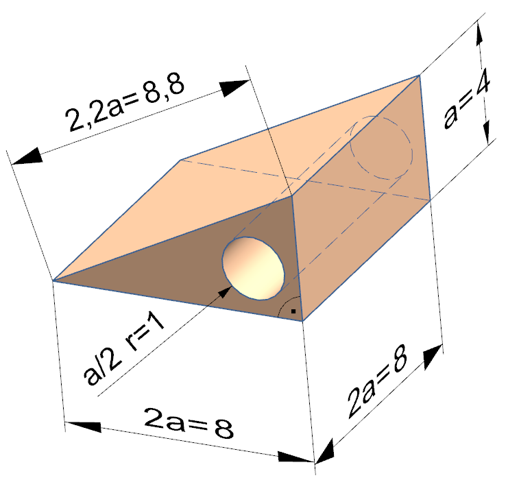
Oh ja stimmt. Ich hatte bei der Oberfläche. Also bei der Bohrung innen die Mantelfläche vergessen. Entspricht ja einem Zylinder. Bei den man die Mantelfläche berechnet. Das gehörte noch dazu. Stimmt !!!
Ich glaube das es immer noch nicht richtig ist ,weil das mit 0,25 meinte er ist falsch ,ehrlich gesagt hab ich auch nicht verstanden was du versuchst hast da zu machen
Naja. Schau doch einfach was du an Flächen hast. Rechne evtl einzeln aus.
3 Rechteckflächen -- Das sollte kein Problem sein.
2 Dreieckflächen -- Sollte man auch rechnen können.
Aber bei den Dreieckflächen geht ja eine Bohrung durch.
Da mußt du also die Kreisfläche abziehen. Achtung es sind 2 Dreiecke.
So dann haben wir innen bei der Bohrung ja noch eine Fläche.
Ist ja quasi eine Mantelfläche eines Zylinders.
Das muß bei der gesamten Oberfläche addiert werden.
Also im Prinzip alles addieren. Nur die Kreisflächen subtrahieren.
Na teil doch mal 1 durch 4. Da sollte 0,25 rauskommen.
Der Durchmesser wird ja a/2 angegeben. Der Durchmesser wäre also 2.
Der Radius von der Bohrung wäre also 1. Das wäre a/4 bzw. 1/4(0,25) von a.
0,25 * a bzw. 0,25 mal 4 = 1. Also da haben wir wieder unseren Radius. 😉
Wie kriegt man die Grafik hin ?