Fläche aus Bauplan/Grundriss berechnen?
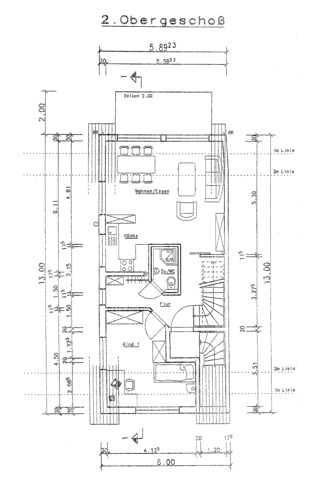
Ich brauche den Flächeninhalt aus dem Raum für Kind 1. Wie kann ich diesen berechnen? Aus der Zeichnung kann ich lesen, dass die linke Seite 450 cm, die untere Seite 412 cm (4.12^5) und die rechte Seite 208 cm lang sind. Für was steht die hochgestellte 5? Nehme an 412,5 cm? Wenn die Zahlen stimmen, die ich gelesen habe, dann fehlen noch die Seiten bei den Schränken, Türe und neben dem Bett.
Ergänzung:
- Soll das ein REALER Grundriss sein?
- Hast Du auch Schnitte dazu?
- Für was brauchst Du den Flächeninhalt? Reine Geometrieaufgabe oder tatsächliche Nutzflächenberechnung nach DIN 277?
Habe leider nur diese Zeichnung. Nutzflächenberechnung.
3 Antworten
Bilde 2 Rechtecke
- der untere Teil mit 4,125 x 2,085
- der obere Teil mit dem Rest bis zu 4,50m (untere Kante der 115-er Wand auf der linken Maßkette)
Jetzt musst Du noch das Dreieck an der schrägen Tür auf der Flurseite abziehen.
Dazu ermittelst Du mit der linken Maßkette die untere Seite der 115er-Wand (obere Ecke der schrägen Wand mir der Tür) und auf der rechten Maßkette den Punkt an der 20er-Wand (untere Ecke der schrägen Wand mit der Tür zur Treppenhauswand).
Die Wand läuft unter 45° so dass Du nun beide Schenkel des Dreicks hast und damit auch die abzuziehende Fläche ausrechnen kannst.
ACHTUNG: Die Nutzfläche ist die RaumINNENseite also nicht die Maße der Achse nehmen oder eben die halbe Wandbreite noch berücksichtigen.
Ich will es nicht vorrechnen. Falls es mit der Beschreibung klappt: gut, falls nicht poste zumindest Deine Rechenversuche 😉😀
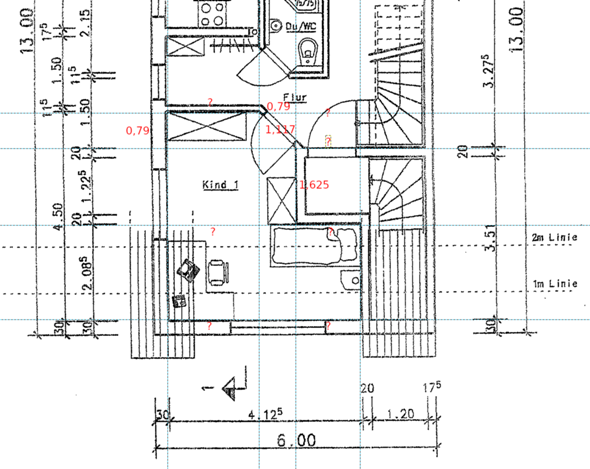
Das untere Fragezeichen verstehe ich nicht. Das untere Rechteck ist ja einfach Breite x Länge, also 6 x 2,085.
Das nächste Rechteck ist bis Unterkante der 115-er Wand. Die Höhe ist einfach mit 4,50 - 2,085. Die Breite holst Du Dir aus dem Treppenhaus rechts. Das Podest von der Terppe von unten hat im Innenbereich die Abmessung von 1,225 x 1,20 m (Deine Linie von der unteren Maßkette bei 4,125 nach oben gezogen), also 4,125 - 1,225 - 0,20 sollte die Breite der restlichen Fläche mit den beiden Schränken sein.
Die Schräge mit der Tür kannst Du Dir über Winkelfunktion, Pythagoras oder ... ermitteln. Daraus ergibt sich dann die Restlänge der 1153r-Wand nach links (obwohl Du die eigentlich nicht mehr brauchst.
Die einzige "Schwachstelle" in der Ermittlung ist das fehlende Maß des Treppenhausaustritts, aber das haben wir über die quadratische Annahme oben erhalten.
Kann leider nicht folgen. Kannst du die Fläche bitte vorrechnen oder wenn du eine Idee hast, wie ich die Länge eines dieser Fragezeichen berechnen kann? Also die Fragezeichen sind auf die Längen der Hilfslinien bezogen, die ich eingezeichnet habe.
Fangen wir mit etwas einfachem an:
die Abmessung an der Stelle, die unter der "1.625" steht ist hergeleitet aus der Treppenbreite von 1,20m (Treppe 1,0m + Treppenauge 0,2m) + Wandbreite 0,2m. Die Treppe läuft um 90° nach links und damit hat das Podest eine Länge (von unten nach oben) von ebenfalls ca. 1,20m (in der Maßkette links als 1,225 dargestellt, wobei das kein Mauerwerksmaß ist). Somit ist die Breite (links-rechts) des Podestes ebenfalls 1,20m + 0,2m (zwischen blauer Linie und dem Treppenaustritt = erster Stufe). Ich denke, das ist Dein Knackpunkt, denn die herleitu8ng geht nicht über die Maßketten sondern Bauabstände.
Damit ergibt sich die Breite des oberen Rechtecks (wo "Kind 1" steht) mit 4,125 m - 1,2 Podest - 0,2m Wand
Länge / Breite der Wand mit der Tür hast Du ja bereits mit je 0,79m ermittelt.
Daraus kann man den Rest leicht ausrechnen.
Ansonsten bleibt es aufgrund der fehlenden Maße wie schon von den beiden anderen geschrieben => messen
Somit ist die Breite (links-rechts) des Podestes ebenfalls 1,20m + 0,2m (zwischen blauer Linie und dem Treppenaustritt = erster Stufe)
Wie kommst du darauf?
"... denn die Herleitung geht nicht über die Maßketten sondern Bauabstände..."
und
"Die einzige "Schwachstelle" in der Ermittlung ist das fehlende Maß des Treppenhausaustritts, aber das haben wir über die quadratische Annahme oben erhalten."
Verstehe aber ich kann da keine Annahmen führen. Ich denke, da muss ich auf der Skizze messen oder direkt an der Stelle. Danke für deine Tipps!
Teilweise musst du die Maße herausmessen, da einige fehlen.
Zu unterscheiden ist bei der Berechnung die ältere DIN 277 (die aber noch immer gilt) oder neueren Wohnflächenberechnung. Gerade bei Dachschägen ist dort der Unterschied immens! Bei der DIN 277 ergibt es mehr m².
Nein die Zahl wurde einfach 4.125 Meter heißen. Die hochgestellte Zahl kommt einfach mit daneber.
Leider ist die Zeichnung schlecht bemaßt und deine gesuchten Größen müssen rausgemessen werden. Ein gutes PDF Programm oder ein cad Programm kann das. Mit der richtigen Skalierung.
Sonst müsste man einfach das abschätzen wenns nicht zu genau sein soll.
Das habe ich nicht ganz verstanden aber bin über die 0,79 auf 1,117 gekommen, indem ich angenommen habe, dass 2 Ecken des Dreiecks 45° sind.
Was meinst du mit Achse?
Mir fehlt eigentlich nur noch 1 Seite. Meine Frage habe ich ergänzt, auf dem Grundriss sind Fragezeichen eingetragen. Wenn ich die Länge nur für eines dieser Fragezeichen habe, dann kann ich die Fläche berechnen.