Federkraft - Kraeftegleichgewicht
Hall liebe Leute ich verstehe das Kraeftegleichgewicht nicht: F1 + F2 = ma = -kx + -kx = -2kx
Angenommen der Block wird nun ein wenig Ausgelenkt, dann ist klar das dieser mit ma zurueck in seine Ruhelage schiesst, ok. Aber wenn er nun sagen wir nach links Ausgelenkt ist dann drueckt doch eine Feder (meinetwegen F1) diesen von sich weg --> F1 ist positiv. Im selben Moment zieht Feder 2 mit der selben Kraft, u da links ausgehend von Ruhelage der Weg (-) ist, ist auch F2 positiv. Also ist doch ma = (+)2kx Wo ist mein Denkfehler?
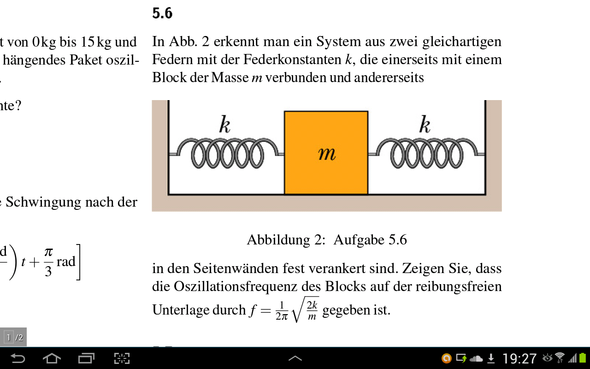
2 Antworten
Gedankenexperiment:
Sie verschieben die Masse schnell nach rechts. Welche Kräfte Wirken? Gegen Sie wirkt kx + kx = 2kx und weiterhin wirkt gegen Sie m * a. Die müssen in der Summe der von Ihnen aufgewendeten kraft F entsprechen. Da das System jedoch eigendynamisch ist und es keine externen Kräfte gibt, setzen Sie Ihre Kraft einfach 0.
Kommt erstmal raus:
2kx + mg = F und da F ja nicht existiert, weil es nur ein Gedankenexperiment war:
2kx = -mg. bzw. 2kx + mg = 0. So sieht prinzipiell der korrekte Ansatz aus, wenn man in Ruhelage den Nullpunkt setzt und nach rechts die Werte positiv werden.
Alles andere ist Murks.
Skizziere die Kraftvektoren auf die Zeichnung, und ein Licht geht auf.
Hallo! Da habe ich jetzt sogar selbst mal eine Frage:
geg.: Feder-Masse-Schwinger
Feder im Koordinatenursprung befestigt, Grad der Freiheiten = 1 in Richtung -x, +x.
An der Feder ist natürlich die Masse befestigt. Ich würde jetzt folgende Kraftvektoren einzeichnen:
Ursprung der beiden Vektoren: Massenschwerpunkt.
Einen Vektor zeigend nach -x mit dem Wert: -c * x, einen zweiten Vektor zeigend nach +x mit dem Wert: m * d²x / dt², einen dritten Vektor (erzwungene Schwingung) zeigend nach + x, mit dem Wert: F(t).
Jetzt würde ich die Gleichung wiefolgt aufstellen:
- c * x = F(t) + m * d²x / dt².
Umgestellt:
m * d²x / (dt)² + c * x = - F(t).
Ist die Vorzeichenkonvention so richtig?
Und ein Problem hätte ich auch noch:
Die Auslenkung x ist immer entgegengesetzt der Kraft.
Ich würde dem widersprechen wollen und fragen, ob ich einem Denkfehler zum Opfer falle!
Auslenkung nach +x, keine erzwungende Schwingung, gleiches Modell.
Dann würde die Feder mit -c * x reagieren und die Masse mit +m * xpunktpunkt. Die Reaktionskraft durch die Masse erzeugt, würde Ihrer Aussage widersprechen. Diese Kraft würde in Richtung +x zeigen. Liege ich falsch?
Hallo
Eine sehr interessante Frage.
Ich würde Folgendes antworten.
Bei Bewegungsfragen stellt man keine Gleichgewichtsbedingung, sondern wird das 2. newtonsches Prinzip angewendet.
F = ma = m * (d²x / dt²)
F ist hier die vektorielle Summe aller Kräfte die auf den Massenpunkt wirken.
Das Elastische Kraftfeld ist definiert durch F = -cx. Dazu die kommt noch F(t) in die positive Richtung. Nach meinem Verständnis ist die Bewegungsgleichung:
-cx + F(t) = m(d²x / dt²)
m(d²x / dt²) + cx = -F(t)
also genau Ihre Gleichung.
Beim Studium des harmonischen Schwingung, geht man von der folgenden mathematischen Gleichung aus:
(d²x / dt²) + (omega)^2 x = 0
Die Lösung dieser Differentialgleichung ist die Harmonische Schwingung. Der Koeffizient von x, muss unbedingt positiv sein, daher das Quadrat. Wenn dieser Koeffizient negativ ist, ist die Gleichung:
m(d²x / dt²) - (lambda)^2 x = 0
Die Lösung dieser Gleichung ist eine Kombination von e-Funktionen, und keine Schwingung mehr. Fand ich interessant.
Vielen Dank für Ihre Antwort und vorallem dafür, dass Sie das "interessant" fanden / finden :).
Tatsächlich bin ich demnächst Mechatronik-Ingenieur, aber eigentlich schon viel zu lange "drüber" über den Abschluss. Sogesehen gehören solche Themen eigentlich der Vergangenheit an. Wie man allerdings sieht, lernt man offenbar nicht aus!
Ich habe interessanterweise vorhin dieselbe Gleichung versucht zu lösen und kam auf Ihr Ergebnis! So.... geht es also tatsächlich NICHT!. Offenbar spielen Dinge wie z.B. das "Rechtssystem" oder das "Linkssystem" bezüglich der Phasenverschiebung der Kräfte, eine elementare Rolle. Ich habe aber zu lange damit nicht mehr hantiert. Das muss sich nun ändern :). Ok... dann nochmals herzlichen Dank, ich werde die Herangehensweise versuchen zu perfektionieren so dass, kein anderer Student diese Frage mehr stellen muss, sofern er meine Ausführung gelesen hat.
Nochmals ganz herzlichen Dank!!!
Mit besten Grüßen,
MTL... anbei eine Private Nachricht!
Über positiv oder negativ wird entschieden über die Achse. Die Auslenkung x ist immer entgegengesetzt der Kraft. Wenn nach links ausgelenkt wird, ist x negativ und F1 + F2 positiv. Wenn nach rechts ausgelenkt wird ist x positiv und F1 + F2 negativ. Also, es gehört ein minus hin, in allen Fällen.