Exponentielles Wachstum - Brauche Hilfe?
Hallo liebe Community,
ich bin stark am verzweifeln bei dieser Aufgabe zu Exponentiellem Wachstum, da ich nur unseriöse Zahlen wie 20 Minuten rausbekommen habe. Könnte mir jemanden helfen und zeigen, wie man zu einem Ergebnis kommt?
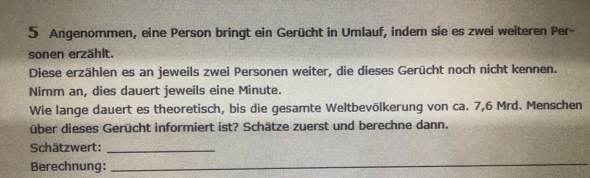
Vielen vielen Dank im Voraus!
5 Antworten
Warum sollen 20 Minuten unseriös sein? Weil Du es Dir nicht vorstellen kannst und Tage oder Monate, vielleicht sogar Jahre geschätzt hast? Beachte:
Wie lange dauert es theoretisch, bis ....
Es handelt sich nicht um ein reales Experiment, sondern um eine mathematische Aufgabe. Um das Experiment in der Realität umsetzen zu können, müsste denjenigen, die das Gerücht gehört haben, sofort zwei Leute zur Verfügung stehen, denen es weitererzählt werden könnte. Außerdem kommt es natürlich darauf an, wie lange man braucht, um das Gerücht wiederzugeben.
Gruß Matti
Wenn du das ganz stupide manuell ausrechnest kommst du auf solche Zahlen ;)
Das was du dabei lernen sollst ist wie massiv man sich bei Exponenten verschätzt. Als das wegen Corona anfing sagten einige das ein Mensch Exponentielles Wachstum nicht richtig verarbeiten kann. Nach dieser Aufgabe sehe ich das auch so.
Kann sein das ich mich verzählt habe aber bei mir kamen 23 Minuten raus. Also die Größenordnung stimmt. Aber rechne das lieber selber nochmal nach ich bin das nur schnell durch gegangen ohne große Sorgfallt da ich die Aufgabe interesant fand.
Es wird wohl angenommen, man erzählt es immer Leuten, die es noch nicht wissen. D.h.,
nach 1 Minute wird es an 2 Personen erzählt,
nach 2 Minuten an 2^2=4 Personen,
nach 3 Minuten an 2^3=8 Personen,
nach n Minuten an 2^n...
Dazu kommen alle, die das Gerücht bereits gehört haben. Dies sind noch einmal
2^n-1. Dies siehst du, wenn du die Entwicklung auf Häuschen-Papier in Türmen darstellst: Die Türme verdoppeln sich ja immer. Wenn du alle Türme bis auf den letzten aufeinander stellst, erhältst du den letzten minus 1.
Nach n Minuten hast du also total 2^(n+1) - 1 Personen. Wie viele Minuten braucht es, bis du bei 7,6 mal 10^9 bist?
Dies kann man im Kopf abschätzen:
2^10 = 1024 = ca. 1000 = 10^3
Also ist 10^30 ca. 10^9
Dann brauchst du noch einmal 3 Verdoppelungen, um auf 8 Mrd. zu kommen. Also 10^33 > 7,6 Mrd.
=> Spätestens nach 32 Minuten wissen es alle.
Heute würde man dies natürlich nicht mehr mit dem Gerücht machen, sondern mit dem Coronavirus. Hier beträgt die Verdopplungszeit der Infizierten weltweit etwa 4 Tage. Also sollten nach etwa vier Monaten ziemlich alle Menschen infiziert sein, die überhaupt infiziert werden können. Das wäre bei ungebremster Ausbreitung Ende April. Bemerkenswerterweise sieht man davon Anfangs April noch kaum etwas. Denn da fehlen ja noch 7 Verdoppelungen, d.h., es ist erst 1 von 10 Mio. Menschen infiziert. Tatsächlich sind es ja heute schon mehr. Aber die Abschätzung zeigt, was noch auf uns zukommen wird, wenn die Uefa weiterhin Fussballspiele mit Publikum spielen lässt.
Einfach den Logarithmus zur Basis 2 benutzen.
2^(x+1)-1 = 7.600.000.000-1
log2(2^(x+1)) = x-1 = log2(7.600.000.000-1)
Zum Verständnis wichtig zu wissen ist noch, dass 2^0 + 2^1 + 2^2 + ... + 2^n = 2^(n+1)-1. Das gilt aber nur für die Zahl 2, wenn das Wachstum irgendeine andere Zahl wäre, müsstest du das wohl einzeln addieren.
Ich hätte auf eine halbe Stunde geschätzt.
Tatsächlich sind es aber 33 Minuten.
32 Minuten. Nach n Minuten wissen es ja 2^(n+1)-1 Menschen.
Nach 0 Minuten 1, nach 1 Minute 3, nach 2 Minuten 7 usw.