Ergebnis der Pq-Formel immer negativ, wieso?
Guten Nachmittag,
Wenn ich die Pq-Formel wie auf dem Bild zu sehen in den Taschenrechner eingebe, kommt als Lösung -10 und - 2 heraus, in der Lösung der Aufgabe steht allerdings, dass man mit der Pq-Formel eigentlich auf ein Ergebnis von 10 und 2 kommen sollte. Ich stehe gerade leider etwas auf dem Schlauch wo ich da den Fehler gemacht habe. Es muss auch 10 und 2 rauskommen, da man nur mit positiven Zahlen weiterreichen kann (ich muss aus diesen beiden Zahlen ja noch die Wurzel ziehen)
Vielen Dank schonmal für eure Hilfe.
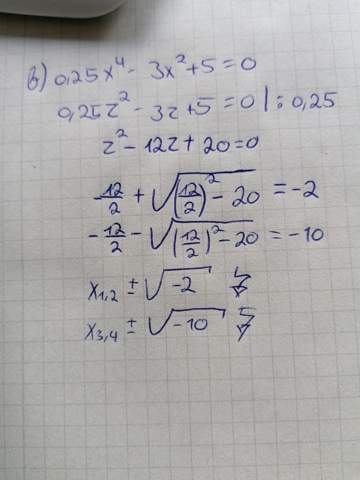
5 Antworten
Ich habe deine Lösungen nicht genau geprüft, aber sie sehen plausibel aus.
Es kann bis zu vier Lösungen geben. Davon sind zwei negativ; die x liegen eben links von 0 auf der x-Achse.
Alles ganz normal.
Nur die Minus unter der Wurzel stimmen nicht, denn 6² - 20 ist größer als 0.
Du hast ganz vorne einen Vorzeichenfehler, die pq-Formel ist -p/2+-Wurzel((p/2)^2-q) und hier ist p=-12.
Mach doch lieber eine quadratische Ergänzung, dann passieren solche Fehler nicht. Also rechne:
z^2-12z+20=0
<=> z^2-2*6z+36=36-20
<=> (z-6)^2=16
<=> z=6+-4
12/2 ± wurzel ((12/2)² - 20)
12/2 ± wurzel (36-20)
12/2 ± wurzel (16)
12/2 ± 4
x1 = 6+4 = 10
x2 = 6-4 = 2
Seit wann ist denn 25:0,25 = 1? Du hast bereits beim Dividieren einen Fehler gemacht. Entweder du teilst durch 25 (dann kommen aber für p und q ziemlich blöde Werte raus) oder du vergendest gleich die Mitternachtsformel.
In der Aufgabe habe ich soweit ich weiß nirgendwo 25:0,25 gerechnet. Ich habe 0,25:0,25=1 gerechnet und das ist soweit ich weiß richtig? Vielleicht ist das 0, auf dem Bild etwas undeutlich oder ich habe etwas unordentlich geschrieben.
Eigentlich hätte man schon darauf tippen können, dass da ein Vorzeichenfehler aufgetreten ist. Und wenn man sich die pq-Formel ansieht, dann ist die Wahrscheinlichkeit hoch, dass der bei
auftritt. Und so IST es auch.
Die Lösung der Gleichung von Ordnung 4 wäre dann am Ende zwar korrekt, aber nur, weil dann das Vorzeichen der vorherigen Rechnung egal wird. Die pq-Formel so wie sie hier angewendet wurde hatte einen Vorzeichenfehler