ein Kreis k geht durch den Punkten A= (1/4) und B=(5/2). Sein Mittelpunkt liegt auf der Geraden g: 5x+ 2y=-15. Wie lautet die Tangente an den Kreis k im Punkt?
ein Kreis k geht durch den Punkten A= (1/4) und B=(5/2). Sein Mittelpunkt liegt auf der Geraden g: 5x+ 2y=-15. Wie lautet die Tangente an den Kreis k im Punkt A?
kann mir wer erklären wie ich das berechnen könnte
1 Antwort
Hallo,
Die Punkte A und B müssen vom Kreismittelpunkt C(Xc|Yc) den gleichen Abstand haben, was sich folgender Gleichung ausdrückt:
Schreibt man die Gleichung in Koordinaten nieder und vereinfacht sie, erhält man folgende Gleichung: 2x - y = 3
Das ist eine Geradengleichung, und zwar die der Mittelsenkrechten der Strecke AB.
Das ist auch einleuchtend, denn alle Punkte die von A und B den gleichen Abstand haben, liegen auf der Mittelsenkrechten von AB.
Die Mittelsenkrechte und die Gerade g schneiden sich im Kreismittelpunkt C.
Um die Koordinaten von C zu berechnen, löst man das LGS
5x + 2y = -15
2x - y = 3
Zum Vergleich: man findet Xc = -1 , Yc = -5, d.h. C(-1|-5) .
Die gesuchte Tangente t geht durch den Punkt A und ist senkreicht zur Geraden (CA).
Man stellt also eine Koordinatenform der Geraden (CA) auf und bestimmt die Gerade t, die durch A geht und zu (CA) senkrecht verläuft.
Zum Vergleich: man findet
t : 2x + 9y = 38
Hier noch eine Zeichnung:
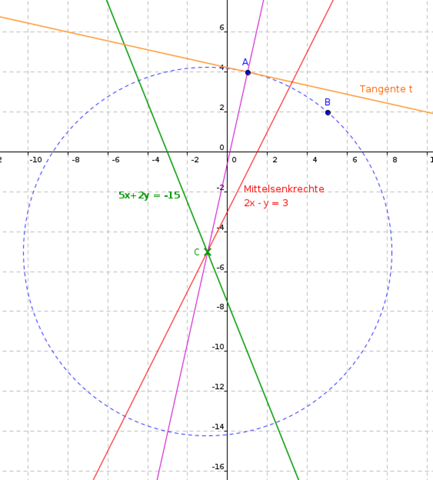
Gruß
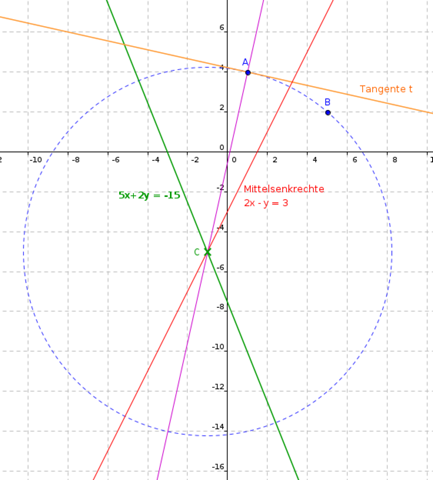
Ok.
Die Koordinaten von C seien (x|y).
Die Koordinaten des Vektors CA lauten (1-x|4-y)
Die Koordinaten des Vektors CB lauten (5-x|2-y)
Die Gleichung |CA|² = |CB|² in Koordinaten lautet
(1-x)² + (4-y)² = (5-x)² + (2-y)² <=>
1 - 2x + x² + 16 - 8y + y² = 25 - 10x + x² + 4 - 4y + y² <=>
-2x -8y + 10x + 4y = 25 + 4 - 1 - 16 <=>
8x - 4y = = 12 | : 4 <=>
2x - y = 3
Das ist die Gleichung der Mittelsenkrechten der Strecke AB.
Setze doch mal die Koordinaten von C(-1|-5) in jede der beiden Gleichungen ein. Beide Gleichungen sind durch die Koordinaten von C erfüllt.
Hier noch der Rest der Rechnung.
Der Vektor CA hat die Koordinaten (1-(-1), 4-(-5)) = (2,9) .
CA ist ein Normalenvektor der Tangente t, also kann man für die Tangentengleichung ansetzen:
t : 2x + 9y = c
Einsetzen der Koordinaten von A(1,4) :
2•1 + 9•4 = c = 38, also lautet die Tangentengleichung
t : 2x + 9y = 38
(Man braucht also die Gleichung der Geraden (CA) nicht bestimmen, sondern kann direkt zur Tangentengleichung übergehen...)
Kannst du mir zeigen wie du auf die gleichung genau gekommen bist : 2x-.=3
2x-y=3