Dritte Wurzel aus -27? Warum "nicht definiert"?
Hallo erstmal,
Bischer hatte ich gelernt, dass 3. Wurzel aus -27 definiert ist, also -3 ergibt, weil ungerade Wurzeln aus negativen Zahlen immer eine Lösung haben. Aber meine Lehrerin meinte, dass man dritte Wurzel aus einer negativen Zahl schon rechnen kann, dennoch ist das nicht definiert. Sie meint, falls wir bei der Arbeit sowas sehen, müssen wir daneben "nicht definiert" schreiben. Ich verstehe es nicht wieso das "nicht definiert" sein soll? (Guckt das Bild bitte an, um zu verstehen, was ich meine) Das ist doch definiert, oder? Was sagt ihr dazu?
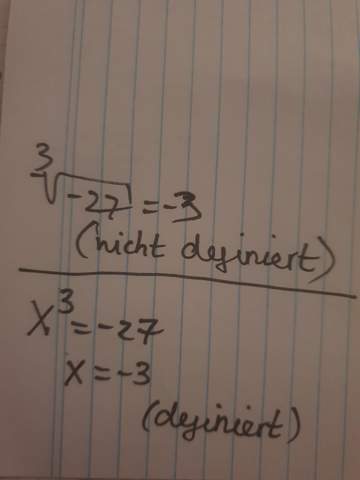
Danke im Voraus
4 Antworten
Die n-te Wurzel aus x stellt dir die Frage: Welche Zahl a ergibt n-mal mit sich selbst multipliziert den Wert x unter der Wurzel?
-3 * -3 * -3 = -27
Die Argumentation für "nicht definiert" folgt aus dem Widerspruch bei der folgenden Rechnung:
-3 = (-27)1/3 = (-27)2/6 = ((-27)2)1/6 = 7291/6 = +3
Als Mathematiker würde ich sagen, dass der Fehler hier bei der (eigentlich nicht zu erlaubenden) Umwandlung der Potenz 1/3 in 2/6 liegt. Das dürfte nicht so erlaubt sein (zumindest bei negativer Basis), weil ja indirekt eine Quadrierung stattfindet und damit die Verpfuschung des Vorzeichens.
Als "in der realen Welt lebender" Mathematiker ist für mich die dritte Wurzel aus -27 definiert.
Siehe dazu den Abschnitt Wurzeln aus negativen Zahlen in der Wikipedia.
nur in Gleichung kann x = -3 sein.
Für Terme wie 3wur(-27) ist -3 nicht definiert.
Nur 3wur(+27) = 3 ist erlaubt.
Solange es keine Gleichung ist , sind Wurzeln immer positiv und Wurzeln aus negativen Zahlen gibt es nicht ( außer man hat die komplexen Zahlen schon erlaubt)
Das ist so festgelegt !
PS : mit den komplexen Zahlen kommt das dieses raus


Das ist so festgelegt ! Das ist dasselbe wie : nicht definiert.
(Solche Frage und das Erstaunen , vielleicht , darüber ,dass das so ist : Ein Dauerthema auch bei GuteFrage.
Wurde vielleicht vorher eine Definitionsmenge für alle Argumente festgelegt?