Dichte den Gitters berechnen?
Hey Leute,
Ich will die Dichte des Salzgitters berechnen, aber ich bin verwirrt wie man das berechnen kann.
Als Ansatz habe ich Dichte=Masse/Volumen.
Masse ist dann die Molare Masse mal die Koordinationszahl (hier vier)
Das Volumen ist das vom Würfel, also a^3, dann soll das der Abstand zwischen die zwei benachbarten Ionen mal zwei und dann mal die Avogadrozahl.
Insgesagt kommt man auf Dichte= M×KZ/(2d(A-B))^3×Na
Ist das jetzt richtig?
2 Antworten
Molare Masse mal Koordinationszahl macht nicht wirklich viel Sinn. Das führt hier nur zufällig zu einem richtigen (vorläufigen) Ergebnis, davon kannst du aber nicht immer ausgehen. Und der Abstand der Teilchen ist völlig egal.
Du hast doch in der Teilaufgabe a) die Summenformel bestimmt. Da solltest du eine Summenformel der Art AB erhalten haben, also genauso viele Teilchen A wie B.
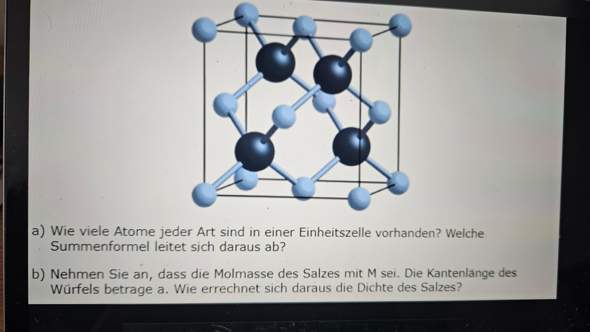
Jetzt schau dir die Elementarzelle, da sind 4 schwarze Kugeln (Teilchen A) drin. Die weißen (Teilchen B) lassen sich ebenfalls zu 4 Stück zusammenfassen, weil die ja nur anteilig da drin sind. Du hast also pro Würfel 4 A und 4 B. Das lässt sich schreiben als 4 AB. Und die haben eine Masse von 4 M, die man über Avogadro in g umrechnen kann, also 4*M*Na. Diese Masse befindet sich in einem Würfel mit dem Volumen a^3. Die Dichte ist also (4*M*Na)/(a^3).
- Du siehst vier fette Kugeln (ich nenne sie A), die ganz innerhalb der Einheitszelle liegen. Also enthält die Einheitszelle vier A-Atome.
- Von den kleinen Kugeln (B) siehst Du acht Stück an den acht Würfelecken kleben. Jedes dieser Atome liegt zu ⅛ innerhalb der Elementarzelle (weil an den Ecken acht davon zusammenstoßen), also macht das insgesamt ein B-Atom.
- Außerdem haben wir noch sechs B-Atome an den Flächen, die liegen zur Hälfte innerhalb der Elementarzelle, das ergibt also weitere 3 B-Atome.
Folglich ist die Summenformel einfach AB, wir haben ja gleich viele Atome von beidem Typ. Die gezeichnete Elementarzelle entspricht übrigens der Zinkblende-Struktur (ZnS).
Um die Dichte aus der Zellkonstanten auszurechnen, erinnerst Du Dich an ρ=m/V. Das Volumen der Elementarzelle ist natürlich V=a³, und bei der Masse berücksichtigen wir, daß vier Formeleinheiten in der Elementarzelle liegen und daß eine davon die molare Masse M und damit die absolute Masse M/Nₐ hat (dabei ist Nₐ die Avogadro-Konstante. Also kommt heraus: ρ = m/V = 4M/(Nₐa³), natürlich muß man beim Einsetzen noch auf die Einheiten aufpassen.