Der Sinus von 60° ist dasselbe wie (die Wurzel aus 3) durch 2?
Hi, ich soll in Mathe folgendes Beweisen:
Sinus 60° = (Wurzel 3) durch 2
(siehe Bild)
Ich hoffe, dass mir jemand weiterhelfen kann.
Hideaki
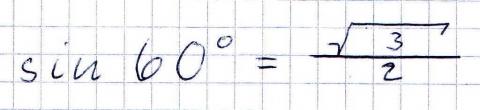
3 Antworten
Stimmt.
Ein gleichseitiges Dreieck hat lauter 60-Grad-Winkel. Der Sinus ist also die Höhe geteilt durch die halbe Seite. Also 1.732/2, also Wurzel von 3 durch 2.
Und wie sieht das dann mit sin30 = 0,5 aus, da kann man ja nicht ein gleichseitiges Dreieck nehmen?
Den Sinuswert ermittelst Du am Besten durch das Ablesen auf der y-Achse auf dem Millimeterpapier. Du wirst ja wohl wissen, wie man da vorgeht!? Der Sinus des Winkels beträgt ca. 0,86. Das ist exakt der Wert 1/2 * Wurzel aus 3. Das gleiche gilt für sin 120°.
Klar! Natürlich musst Du dafür die Sinuskurve "aufmalen" und entsprechend anzeichnen und, die Aufgabe lösen-1/2 * Wurzel aus 3. ! Sin 60°=Sin 120°=1/2 * Wurzel aus 3
gleichseitiges dreieck; mit Pythagoras dann a²=(a/2)²+h² also h²=a²-a²/4 also h=a/2 mal wurzel 3 und dann sin60°=h/a und jetzt h einsetzen, ergibt wurzel aus 3 /2 und bei 30° musst du oben den halben gamma nehmen, der ist 30° und dann sin30°=(a/2):a und sin30°=0,5 gruß ej
Vielen vielen Dank hat mir echt weiter geholfen.
Korrektur: Der Sinus ist Höhe : Seite (nicht halbe Seite). Das andere stimmt. sin 60o = 0,866.
Beweis: Pythagoras: Das gleichseitige Dreieck wird der Höhe nach zerschnitten. Die grösste Seite wird jetzt 2 genannt-> das Quadrat darüber ist also 4. Die kleinste Seite ist dann 1 und das Quadrat darüber auch 1. Da bleibt für das durch die Höhe gebildete Quadrat noch 3, die Höhe ist also Wurzel 3. Der Sinus von 60o ist also Wurzel 3 durch 2,