Coulombkraft von zwei Vektoren?

So, jetzt hier, "Physik 2", oder was? Draußen warm, innen kalt. Was heißt das? Naja gut, zunächst erstmal gar nichts. Folgende Aufgabe gilt es zu lösen

Ansatz

Ich weiß dass r_1,2 dasselbe ist wie r_2 - r_1 und | r | dasselbe wie die Wurzel aus r_x² + r_y². Also erstmal die Formel umschreiben. Dann steht da:

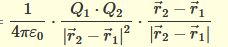
So weit, so (un-)gut. Aber jetzt geht die Action los.

1/4π E_0 ist 1/ 4 π * 8,85 * 10^-12 = 8991804694.

Jetzt zum zweiten Bruch: Erstmal der Nenner. Das wäre getreu dem Motto von Pipi Langstrumpf Q1 * Q2 = 3e * 3e. Ein "e" ist 1,6*10^-9. Also 3 * 1,6*10^-19 * 3 * 1,6*10^-19 = 2,304 * 10^-37

So, jetzt zum Nenner. Der Nenner wäre r_2 minus r_1 zum Quadrat. Ich weiß dasss ich Vektoren voneinander substrahiere, indem ich die Komponentenquadrate substrahiere, also jeweils (-3) - 3 rechne. Kommt -6 bei raus. Dann ist der neue Vektor (-6,-6). Davon jetzt den Betrag wäre die Wurzel aus (-6)² + (-6)² = 6√2 und das dann hoch 2 wäre 72. Also wäre der zweite Bruch nichts anderes als 2,304 * 10^-37 geteilt durch 72

So, jetzt zum dritten Bruch. Da steht jetzt oben im Nenner: r2 - r1. Das wäre ja dann wieder der Vektor (-6,-6). Aber das ist doch ein Vektor! Wie soll ich denn einen Vektor in einem Bruch unterbringen? Außerdem steht doch im Nenner dasselbe wie im Zähler, nur als Betrag. Wenn ich eine Sache durch sich selbst teile, kommt doch dann immer "1" bei raus. Wozu dann der ganze Zauber? Und was ist mit F_2,1 gemeint? Wenn ich die Formel rechne, kommt doch dann ein Zahlenwert raus und kein Vektor. Wie soll man das im Koordinatensystem einzeichnen?

Je suis verwirrté

Answer 1

[AMG38]

Der dritte Term in der Gleichung ist der Einheitsvektor, man sagt auch "normierter Vektor". Das macht man, indem man den Vektor durch seine Länge teilt und die Länge des Vektors ist der Betrag des Vektors.

Da der selbe Betrag als Nenner im zweiten Term ebenfalls vorkommt, kannst du das dort gleich hoch 3 nehmen und dir etwas Arbeit ersparen.

$F=\frac{1}{4\pi\epsilon_0}\cdot\frac{q_1\cdot q_2}{\left|r_2-r_1\right|^3}\cdot\left(r_2-r_1\right)$

Außerdem steht doch im Nenner dasselbe wie im Zähler, nur als Betrag.

Das "nur als Betrag" macht eben den Unterschied, weil es dann nicht dasselbe wie im Zähler ist. Der Betrag eines Vektors ist kein Vektor mehr.

Im Zähler steht also ein Vektor, im Nenner hingegen eine einfache Zahl, in dem Falle:

$\left|r_2-r_1\right|=\sqrt{\left(-6\right)^2+\left(-6\right)^2}=6\sqrt{2}$

(ist übrigens nichts weiter als Pythagoras)

Dann:

$\frac{r_2-r_1}{\left|r_2-r_1\right|}=\frac{1}{6\sqrt{2}}\cdot\binom{-6}{-6}=\binom{-\frac{\sqrt{2}}{2}}{-\frac{\sqrt{2}}{2}}$

Dieses Ergebnis wäre das Resultat vom dritten Term in der Gleichung (die ungekürzte Variante, die du als Screenshot geteilt hast). Das multipliziert mit den restlichen zwei Termen ergibt dann als Lösung weiterhin einen Vektor.

Comments

[Jensek81]

Danke für die Antwort, AMG38.

Ich komme jetzt auf dieses Ergebnis: https://ibb.co/T0st8mP

Das erscheint mir doch etwas komisch. Hab ich da irgendwo einen Denkfehler gemacht. Vorallem: Wie soll ich das ins Koordinatensystem einzeichnen?

[AMG38]

@Jensek81

Die Ladungen kannst du ja zunächst in das Koordinatensystem einzeichnen.
Ladung 1 hat als Koordinate x = 3, y = 3
Ladung 2 hat als Koordinate x = -3, y = -3

Bei deiner Rechnung komme ich allerdings auf ein anderes Ergebnis. Mein Vektor hat am Ende folgende Werte:

-2,033 * 10^(-29)
-2,033 * 10^(-29)

Um diesen in das Koordinatensystem einzuzeichnen, würde ich den Vektor normieren.

Erstmal der Betrag:

|F12| = Wurzel [ (--2,033 * 10^(-29))^2 + (-2,033 * 10^(-29)) ^2) ] = 2,876 * 10^(-29)

Dann daraus den Einheitsvektor:

1 / 2,876 * 10^(-29) * ( -2,033 * 10^(-29), -2,033 * 10^(-29) ) = ( -0,7, -0,7 )

Zum zeichnen würde ich diese Punkte zu den Koordinaten der Ladungen addieren.

D.h. einen Punkt machst du bei

x = -3,7, y = -3,7 und verbindest den Mittelpunkt von Ladung 1 mit dieser Koordinate.

F21 hat ein umgekehrtes Vorzeichen, also
x = 3,7, y = 3,7

Diesen Verbindest du mit dem Mittelpunkt der Ladung 2.

Am Ende gucken die Pfeile dann entgegengesetzt, d.h. die Ladungen stoßen sich ab.

Ob das die genaue Vorstellung deines Lerhres/Dozenten ist, kann ich leider nicht beurteilen. Kannst ja gerne im Nachgang schreiben, ob es richtig oder falsch war.

[Jensek81]

@AMG38

Danke für die ausführliche Antwort. Aber eines verstehe ich noch nciht. Wieso soll ich einen Punkt bei x = -3,7 und y = -3,7 machen, wenn der Vektor doch (-0,7, - 0,7) ist. Soll das dann nicht eher x = -0,7 und y= - 0,7 heißen?

Answer 2

[RitterToby08]

Den Vektor lässt du einfach stehen. Das hier ist nur ein Skalar mutipliziert mit einem Vektor. Die Notation ist vielleicht verwirrend. Sie bedeutet lediglich, dass du 1/(|r2-r1|) mit dem Vektor multiplizierst.

Es kommt auch nicht 1 raus, da du nicht zwei Zahlen multiplizierst. Das Ergebnis wird aber ein Vektor der Länge 1 sein.

Answer 3

[Reggid]

1/4π E_0 ist 1/ 4 π * 8,85 * 10^-12 = 8991804694.

nein, denn diese größe ist nicht dimensionslos, sondern hat (in SI einheiten) die dimension Nm²/C²

Ein "e" ist 1,6*10^-9

nein. ein e ist ist 1,6*10^-9 C. dementsprechend ist auch der zähler nicht dimensionlos, sondern hat die einheit C²

Also wäre der zweite Bruch nichts anderes als 2,304 * 10^-37 geteilt durch 6√2

nein, du hast das quadrat im nenner vergessen. außerdem ist der bruch nicht dimensionslos, sondern hat die einheit C²/(inwasauchimmerRgegebenist)²

Aber das ist doch ein Vektor!

ja natürlich ist das ein vektor. die kraft ist ein vektor. wäre schlimm wenn da kein vektor rauskommen würde.

Wie soll ich denn einen Vektor in einem Bruch unterbringen?

Wie soll ich denn einen Vektor in einem Bruch unterbringen? Außerdem steht doch im Nenner dasselbe wie im Zähler, nur als Betrag. Wenn ich eine Sache durch sich selbst teile, kommt doch dann immer "1" bei raus.

du teilst aber nicht eine sache durch sich selbst. sondern einen vektor durch seinen betrag. das resultat ist ein einheitsvektor in die entsprechende richtung.

Und was ist mit F_2,1 gemeint?

die kraft die ladung 2 auf ladung 1 ausübt. im gegensatz zur kraft die ladung 1 auf ladung 2 ausübt.

Wenn ich die Formel rechne, kommt doch dann ein Zahlenwert raus und kein Vektor.

da kommt ein vektor raus (ein teil deiner eigenen frage war ja gerade warum da vektor im zähler steht)

Woher ich das weiß: Berufserfahrung – Physiker (Teilchenphysik)