brüche kürzen (bitte beschreibung lesen)
das ist keine hausaufgabe. ich habe den selben bruch unterschiedlich gekürzt und komme zu unterschiedlichen ergebnissen und möchte fragen wieso. und selbst wenn das eine hausaufgabe wäre, es ist eine eigenleistung vorhanden und somit wäre die frage erlaubt
ich habe zwei bilder hochgeladen. im ersten bild habe ich den bruch ganz normal gekürzt.
im zweiten bild habe ich den selben bruch zuerst verändert und dann gekürzt. und zwar habe ich beim zähler das b ausgeklammert und dann den bruch gekürzt. aber ich komme zu unterschiedlichen ergebnissen. wieso? habe ich ein fehler gemacht?
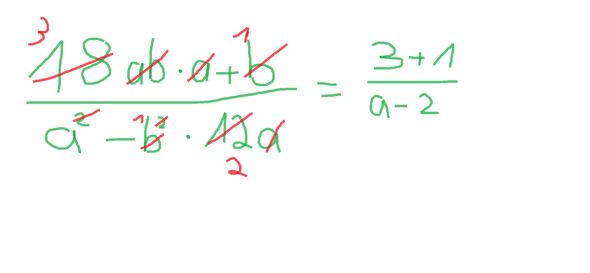
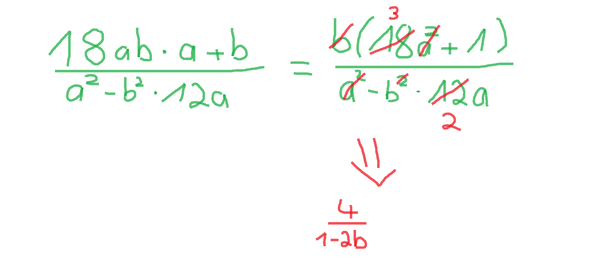
6 Antworten
Beide Rechnungen sind falsch.
A. Gekürzt werden können nur Faktoren, nicht Summanden.
Faktoren können durch Ausklammern neu enstehen, wenn der neue Faktor dann allen Summanden im Zähler oder Nenner gemeinsam sind.
Wenn keine Klammer stehen, lässt sich überhaupt nichts kürzen:
Der Zähler hat zwei Summanden, nämlich 18 aba und b.
Also kann nur b augesklammert werden.
Die Summanden a und -b12a im Nenner haben aber diesen einzigen im Zähler ausklammerbaren Faktor nicht gemeinsam.
Umgekehrt haben die Summanden des Zählers den einzigen im Nenner ausklammerbaren Faktor a nicht gemeinsam.
(18aba + b) / (a - b 12 a) =
(18a²b + b) / (a² - b² 12 a) =
( b(18a² + 1) ) / ( a (a - 12b² ) ); ⇒ unkürzbar.
B. Ich vermute, dass in der Original-Aufgabe einige Klammern stehen: (wobei der Nenner bei gewöhnlicher Bruch-Schreibweise nicht in Klammern zu stehen braucht, hier aber schon). Dann lässt sich schon etwas kürzen:
18ab(a + b) / ( (a² - b²) 12 a) =
a kürzen, dritte binomische Formel anwenden, Zahlen in Faktoren zerlegen:
3 * 6 * (a + b) / ( (a - b) (a +b) 2 * 6) =
3 (a + b) / ( (a +b) (a - b) 2 ) =
3 / ( 2 (a-b) )
C. Hilfe: Schreibe erst die ausgeklammerte Form ausführlich hin, und kürze erst, wenn du sicher bist, dass du in Zähler und Nenner lauter Faktoren vor dir hast und keine Summanden mehr.
Lehrer machen es manchmal schon so, dass sie "Summen kürzen", weil sie den Zwischenschritt des Ausklammerns stillschweigend voraussetzen und übergehen. Das sollte aber nur tun, wer sich schon entsprechendend sicher ist.
Der "wichtige Punkt" ist, dass sich ausschließlich Faktoren kürzen lassen.
Wenn das durchgedrungen ist, erfüllte mein ellenlanges Blabla seinen wesentlichen Zweck.
Korrekt. Vollständige Rechnung
(18ab)/(a²-b²) : (12a)/(a+b)
= (18ab)/(a²-b²) * (a+b)/(12a)
= 18ab * (a+b) / (a²-b²) / 12a
= 1,5b * (a+b) / (a²-b²)
= 1,5b * (a+b) / ((a+b)*(a-b)) | Erweiterung dritte binomische Formel
= 1,5b * (a-b)
(wenn man ":" als Hauptbruchstrich nimmt).
Tippfehler von mir mal wieder:
"(18aba + b) / (a - b 12 a) =
(18a²b + b) / (a² - b² 12 a) = "
Es muss in der erste Zeile natürlich auch heißen
"(18aba + b) / (a² - b² 12 a) = "
...warum motzt keiner?
Es ist kein Wunder: Wenn Du beim Kürzen massenhaft Fehler machst, wäre es eher erstaunlich, beidesmal das gleiche Ergebnis zu erhalten.
Rechne mal schön schrittweise und schreibe alle Einzelschritte auf, vielleicht kann Dir dann jemand Deine Fehler erklären.
Hint: Kürzen heisst, den ganzen Zähler und den ganzen Nenner durch denselben Ausdruck zu teilen.
Oder eine Stufe einfacher: Differenzen und Summen kürzen nur die Dummen.
ich finde keine fehler. was habe ich den z.b. falsch gekürzt?
ok wenn ich den bruch normal kürze, komme ich auf 3b/2(a-b)
wenn ich zuerst b im zähler ausklammere, komme ich auf
4/2(a-b)
Beides ist immer noch absurd falsch. Wodurch kürzt du denn im ersten Fall?
Ja, aber das ist auch nicht besser. Mit "schrittweise" ist gemeint, dass Du jeden Zwischenschritt einzeln aufschreibst - dann kann man auch den Finger drauflegen und sagen, genau hier hast Du den Fehler gemacht.
So, wie es auch im neuen Bild aussieht, kann man nur sagen:
1) Das Ergebnis stimmt nicht. Schon deshalb nicht, weil der Ausdruck überhaupt nicht gekürzt werden kann.
2) Du hast vermutlich vergessen, dass ausschließlich Faktoren aus einem Produkt (das wäre das, was nach Ausklammern entsteht) gekürzt werden dürfen.
Beispiel: (3 * a * b + 4 * a * c) ist eine Summe, und darf nicht gekürzt werden.
Nach Ausklammern ergibt sich:
a * (3 * 1 * b + 4 * 1 * c) = a * (3b + 4c)
Das ist ein Produkt und darf gekürzt werden, sofern man im Nenner ein Produkt mit geeignetem Faktor hat.
sofern man im Nenner ein Produkt mit geeignetem Faktor hat.
Das heisst, wenn auch dort a oder (3b + 4c) vorkommt, bzw. eine Potenz davon.
ich habe den selben bruch unterschiedlich gekürzt und komme zu unterschiedlichen ergebnissen und möchte fragen wieso
Merksatz: In Differenzen und Summen kürzen nur Menschen mit unterentwickeltem intellektuellem Potential.
wieso? habe ich ein fehler gemacht?
Du hast Deine w-Frage selbst beantwortet. Du hast einen Fehler gemacht. Und dies ist sehr verharmlosend ausgedrückt, ich tippe eher auf ein: Du hast es nicht verstanden.
Du kürzt nach dem Motto: Wenn der Bruch 16/64 ist kann ich in Zähler und Nenner die 6 wegstreichen. Dies funktioniert nur bei ganz wenigen Brüchen, ein Beispiel habe ich Dir gegeben.
Es gibt zwei Möglichkeiten: Entweder du hast die Brüche falsch aufgeschrieben oder du kürzt falsch.
Nehmen wir den Zähler. Meinst du wirklich
18 ab * a + b? Das ist dann ja 18a²b + b, da kannst du b ausklammern und bekommst
b(18a² +1). Dann kannst du aber nicht mit 6 kürzen, da die 6 ja gar nicht ausgeklammert werden kann.
oder meinst du
18ab (a+b)
Dann kannst du natürlich durch 6 kürzen.
b(18a² +1). Dann kannst du aber nicht mit 6 kürzen, da die 6 ja gar nicht ausgeklammert werden kann.
achso man kann die werte im klammer nicht kürzen?
Du kannst nur das kürzen, was du aus einer Summe ausklammern kannst. Mehr nicht.
Hast du denn die Klammern richtig gesetzt? Oder hast du da was weggelassen.
STIMMT ich habe die aufgabe flasch aufgeschrieben
die orginale aufgabe war
(18ab)/(a²-b²) : (12a)/(a+b)
diesen bruchterm soll gekürzt werden. zuerst macht man den kehrwert
(18ab)/(a²-b²) * (a+b)/(12a)
und jetzt kann man den bruchterm gut kürzen
am ende kommt 3b/2(a-b) raus