Bis wie viel Grad spricht man von Kleinstwinkeln?
Hallöle, habe morgen Physik mündlich o_0 Bei einer Formel hier geht man davon aus, dass der tan von Kleinstwinkeln ungefähr gleich dem sin von Kleinstwinkeln ist. Weiß jemand bis zu welchem Winkel man davon sprechen kann?
4 Antworten
Die Ursache sieht man schön in der Reihenentwicklung beider Funktionen:
sin(x)=x-x^3/6+x^5/120-x^7/5040+x^9/362880-...
tan(x)=x+x^3/3+x^5*2/15+x^7*17/315+x^9*62/2835+...
wobei x in der SI-Einheit rad vorgegeben ist.
Die veraltete Einheit ° ist um den Faktor 180/Pi größer -> also schauen wir uns die Differenz-Funktion an:
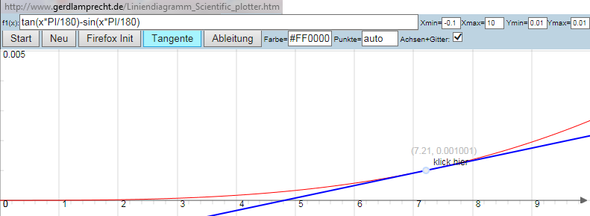
tan(x*PI/180)-sin(x*PI/180) siehe Bild
http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm
In der Schule reicht meist eine Genauigkeit von 3 Nachkommastellen (viel genauer sind viele Billig-Taschenrechner auch nicht!).
Bei 7.21 ° ist diese Grenze erreicht (Tangente funktioniert nur, wenn Punkte=auto)
Oft rundet man auf und sagt: bei Winkel kleiner 10° sind die Differenzen der Funktionen sin(x) und tan(x) vernachlässigbar klein.
Wenn der Winkel kleiner gleich 10° ist, kann man die Kleinwinkelnäherung benutzen.
Das kommt darauf an, was du unter "ungefähr gleich" verstehen willst.
Weil tan(x) = sin(x) / cos(x) ist, ist tan(x) genau dann "ungefähr gleich" sin(x) wenn cos(x) "ungefähr gleich" 1 ist
cos(1) = 0,99985 ca. 0,015%
cos(2) = 0,99939 ca. 0,06%
cos(3) = 0,99863 ca. 0,14%
cos(10) = 0,98481 ca.1,5%
cos(20) = 0,93969 ca. 6%
(Winkel in Grad gemessen, Vollwinkel = 360°)
Also auf jeden Fall bei Epsilon. ;-))