Biquadratische Gleichung mit Komplexen Lösungen?
Hallo zusammen,
ich habe eine biquadratische Gleichung, und am Anfang wende ich die Substitution an. Ich erhalte zwei Lösungen, ähnlich wie in der Lösung u1 und u2. Bis dahin alles klar. Jetzt wandele ich sie in die trigonometrische Form um, indem ich arctan(IM/Re) verwende. Davor berechne ich natürlich den Betrag von u1, der sich als 2 ergibt. Jetzt rechne ich das Ganze aus und komme auf 120 Grad.
Im zweiten Bild im Anhang seht ihr zwei Darstellungen. Da man die Wurzel aus 2 ziehen muss, weil das ursprüngliche x2 = u ist, kommt man auf cos 60 Grad + i sin 60 Grad. Das konnte ich mir noch herleiten, weil tan ja das Verhältnis zwischen Sinus und Kosinus ist. Aber woher kommen plötzlich die 240 Grad in der zweiten Lösung für u1? HÄÄÄ xD Ich stehe auf dem Schlauch und hoffe, ihr könnt mir weiterhelfen.


2 Antworten
phi1 = arctan(sqrt(3)/-1) + 180° = 120°
phi2 = arctan(-sqrt(3)/-1) + 180° = 240°
Die Wurzel aus phi1 hat die beiden (Winkel-)Lösungen:
120°/2 = 60° und 60° + 360°/2 = 240°
Die Wurzel aus phi2 hat die beiden (Winkel-)Lösungen:
240°/2 = 120° und 120° + 360°/2 = 300°
Macht durchaus Sinn. Angenommen z liegt bei einem Winkel von phi. Dann liegt die n-te Wurzel von z zunächst bei phi/n und weitere Lösungen bei phi/n zusätzlich einem Vielfachen von 360°/n. Bei dieser Aufgabe ist n=2.
Danke für den Stern.
Bei der ersten Lösung habe ich die 120Grad die schreibe ich ja als Wurzel aus 2 x (COS 60 + i x sin60) aber warum wird bei den 240 Grad zwei mal der volle Wert in der Rechnung für Sinus und Cosinus genutzt? Wurzel aus 2 x (cos 240 + i x sin 240) ?? Dachte tan ist die differenz
Hab die Änderung in den Lösungen überarbeitet damit ihr vollständigen Einblick habt. Grüße
Nein für U1 gibt es zwei Lösungen und für U2 gibt es auch wieder zwei Lösungen
X1= Wurzel aus 2 x (cos 60 + i x sin 60) x1.2 = Wurzel aus 2 x (cos 240 + i x sin 240) und für u2= -1-iWurzel3 = X2 = Wurzel2 x (cos 120 + i x sin 120) usw..
Vielleicht hilft ein Blick auf den Einheitskreis:
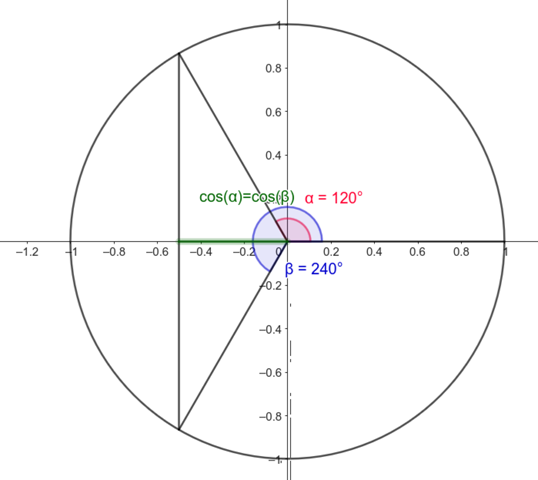
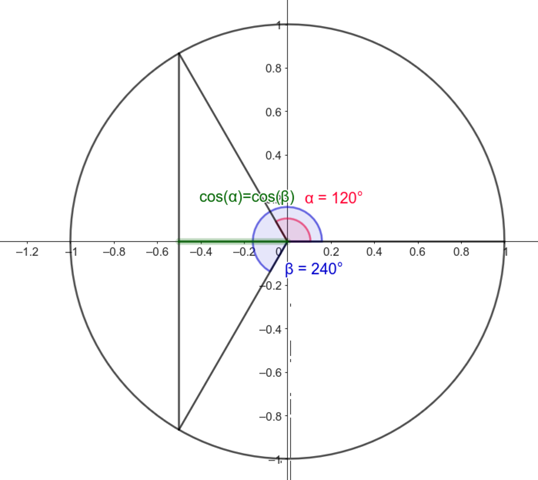
240Grad/2 = 120grad und 120 + 360 /2 = sind 240 Grad also irgendwie macht das keinen sinn