Könnt ihr mir bitte bei der Aufgabe helfen?
Bestimme grafisch die Stellen, an denen die Funktion f mit der Gleichung
(1) y=x²+1
(2) y=x²-3
(3) y=x²-4
den Funktionswert -3 annimmt.
Ich bin eigentlich nicht schlecht in Mathe und quadratische Funktionen liegen mir auch gut, aber hier komme ich einfach nicht weiter. Danke für die Hilfe im Vorraus!
3 Antworten
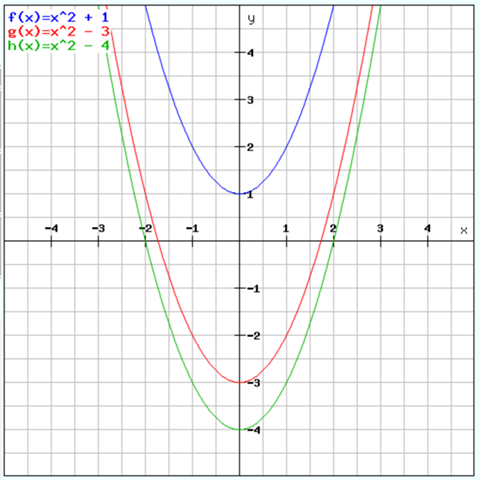
So sehen die Parabeln aus (eigentlich sollte zum Rüstzeug eine Schablone für eine Parabel gehören)
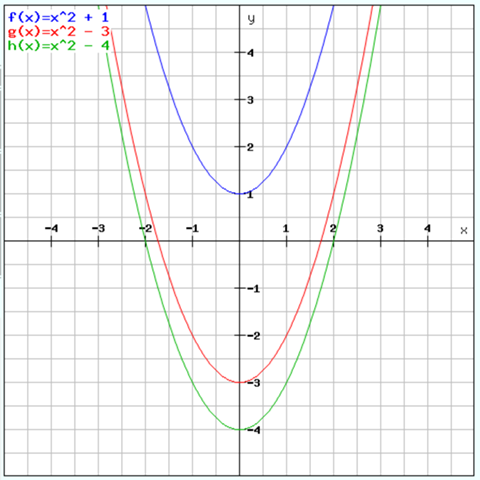
1)
f(x) = x^2 + 1
f(x1) = -3
x1 = es gibt keine Lösung
2)
f(x) = x^2 - 3
f(x2) = -3
x2 = 0
3)
f(x) = x^2 - 4
f(x3) = -3
x3 = ± 1
Danke dir, du warst meine Rettung. Jtz habe ich auch verstanden wie das geht.
Achso und noch eine Frage, kann man das auch Berechnen zb: mit einem Taschenrechner?
Ja, ich führe es mal an der dritten Parabel vor:
f(x) = x^2 - 4
Nun soll der Funktionswert = -3 sein, also setzen wir an:
f(x) = -3 = x^2 - 4
und lösen -3 = x^2 - 4 nach x auf:
x^2 = -3 + 4 = 1
x = √1 = ± 1
zeichne die Parabel
y = x² + 1
den Funktionswert -3 (y-Wert) wird sie nie annehmen; das siehst du dann.
sicher das sie nie den wert -3 annimmt? Das heißt die Aufgabe ist eine Irreführung?
Das ist keine Irreführung; es gibt einfach keine x-Stelle für den funktionswert -3 weil die parabel nach oben geöffnet und um 1 nach oben verschoben ist. - Du musst von -3 auf der y-Achse waagerecht zur Parabel "gehen" und gucken, welcher x-Wert es ist.
Mal sehen, was du bei (1) rauskriegst ;-)
Achso und noch eine Frage, kann man das auch Berechnen zb: mit einem Taschenrechner? Denn in der Aufgabe steht noch das man es noch durch eine rechnung kontrollieren kann.