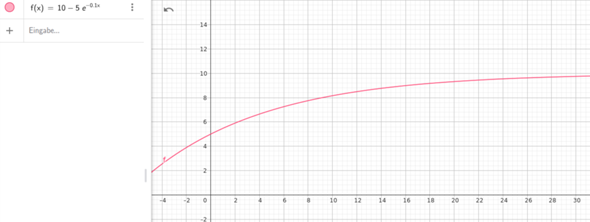
Beschränktes Wachstum?

Hallo zusammen,

Ich habe eine Frage zu den Formeln von Beschränktem Wachstum und beschränktem Zerfall und zwar lauten die Formeln f(t)=S-c•e^-k•t für beschränktes Wachstum und f(t)=S+c•e^-k•t. Warum addiert man nun beim beschränkten Zerfall also was ändert sich da?

Danke schonmal im vorraus

Answer 1

[pchem]

Beschränktes Wachstum:

$f\left(t\right)=S-c\cdot\exp\left(-k\cdot t\right)$

Schauen Sie sich an, wie sich die verschiedenen Bestandteile verhalten: S ist eine Konstante also bleibt immer gleich. Der Term "c•exp(-k•t)" ist für t = 0 gleich c:

$c\cdot\exp\left(-k\ \cdot0\right)=c\cdot\exp\left(0\right)=c\cdot1$ D.h. zum Zeitpunkt t = 0 wird von S genau c abgezogen. Wenn nun t immer größer wird, nähert sich "exp(-k•t)" immer mehr der Null an. D.h. für sehr hohe Zeiten wird von S fast nichts mehr abgezogen.

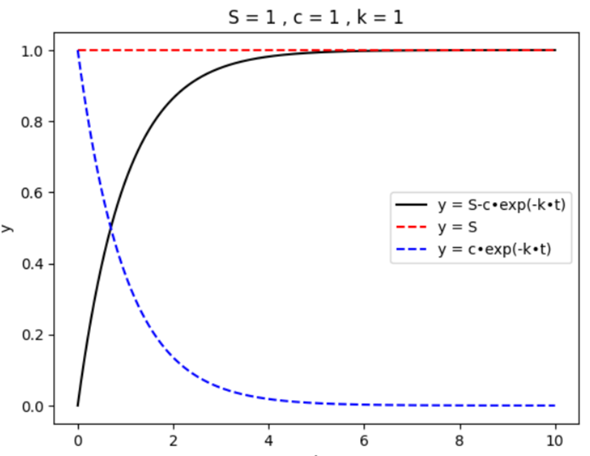
Hier sind einmal die verschiedenen Bestandteile der Funktion dargestellt, wobei für S, c und k als Beispiel jeweils 1 eingesetzt wurde:

Für den beschränkten Zerfall ist das dann entsprechend anders.

Answer 2

[MichaelH77]

die beiden Formeln unterscheiden sich nur durch das Vorzeichen der Konstante c

S ist die Schranke, an die sich das Schaubild langfristig annähert

beim Zerfall wird immer was dazu addiert, was aber immer kleiner wird, je größer t wird. Also Annäherung von oben an die Schranke

beim Wachstum wird von der Schranke immer was abgezogen. Auch hier wird das, was subtrahiert wird, immer kleiner, je größer t wird. Also Annäherung von unten an die Schranke