Berechnen Sie, bei welcher Produktionsmenge die Zunahme der Gesamtkosten minimal ist. Wie hoch ist dann die Zunahme?
Hallo,
ich komme bei einer Aufgabe aus meinem Mathematik Buch nicht weiter und weiß keinen Lösungsansatz.
Die Frage lautet: „Berechnen Sie, bei welcher Produktionsmenge die Zunahme der Gesamtkosten minimal ist. Wie hoch ist dann die Zunahme?“
Eine Kostenfunktion habe ich schon. Diese lautet: K(x): 0,3x^3+17,5x^2+30x+1000
Vielleicht kann mir ja jemand weiter helfen. Vielen Dank schonmal.

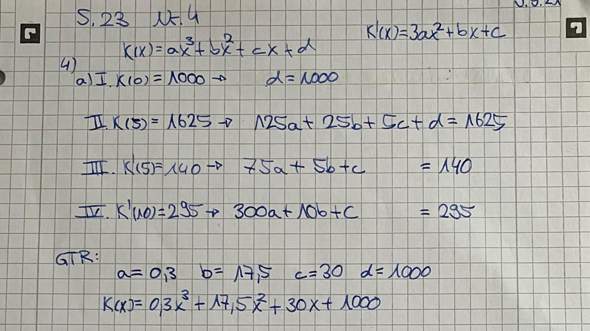
.
6 Antworten
Aufgabe a) Ich nehme für die Kostenfunktion eine Parabel an, ich weiß aber nicht warum!
Maximale Produktionsmenge beträgt 20 heißt, die Funktion ist nur im Intervall von 0 bis 20 gültig.
Fixkosten betragen 1000, also: K(x) = ax³ +bx² +cx + 1000
Bei x = 5 sind die Gesamtkosten 1625. Also K(5) = a*5³ +b*5²+c*5 + 1000 = 1625
Grenzkosten bei x = 5 sind 140 also K'(x) = 3a5² + 2b*5+c = 140
Bei einer Produktionsmenge von x = 10 beträgt die Änderungsrate 295 also K'(10) = 3a10² + 2b*10+c = 295
Die Gleichungen heißen:
125a+25b+5c+1000=1625
75a+10b+c=140
300a+20b+c=295
Lösung: a = 1 und b = -7 und c = 135
(Beim Vergleich mit deiner Lösung fällt auf, dass du die Ableitung K'(x) falsch hast. Aus bx² wird 2*b*x und eingesetzt mit x = 5 dann 10b)
K(x) = x³ -7x² +135x + 1000
c) Wo ist die Zunahme minimal?
Minimum(3x² -14x +135) = .... im Produktionsintervall 0 bis 20
Minimum feststellen mit 2. Ableitung von K(x)
K''(x) = 6x - 14 = 0
x = 14/6 = 7/3 = 2,333 (sogar im Intervall 0 bis 20! :)
Wie hoch ist die Zunahme der Kosten?
K'(2,333) = 3(2,33)² -14*(2,33) +135 = ....
d) K(x = 4) = ....
K'(x = 4) = .....
K''(x = 4) = .....
Aufgabe e) K(x) = x³ -7x² + cx +1000
K'(x) = 3x² -14x + c
K'(x=5) = 75 -70 + c = 137
c=132
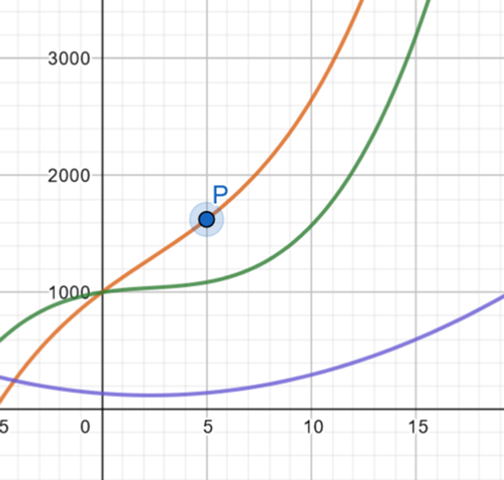
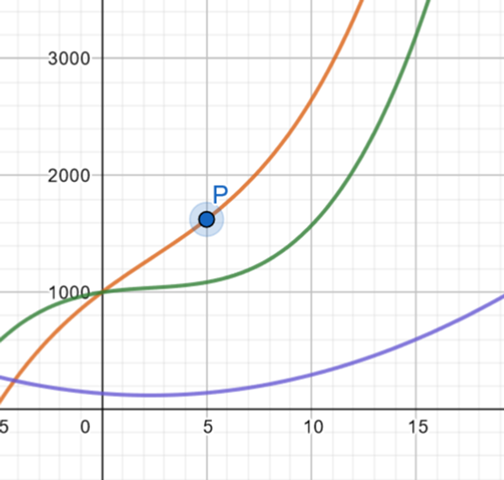
Was allerdings nun unlogisch ist, dass aufgrund der Datenpanne die Kosten gesunken sind...(grüne Kurve ist die neue K(x) und die orangene ist die alte K(x)
Vielen Dank. Das hat mir wirklich weiter geholfen. 🙏🏼
Hallo,
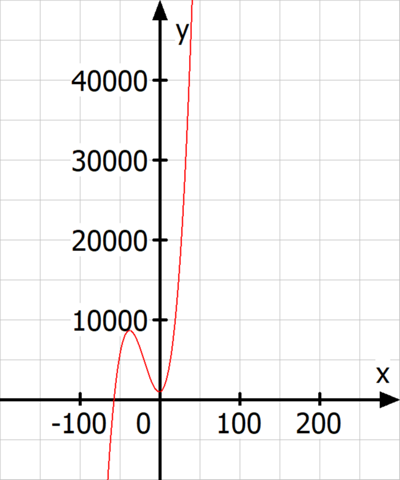
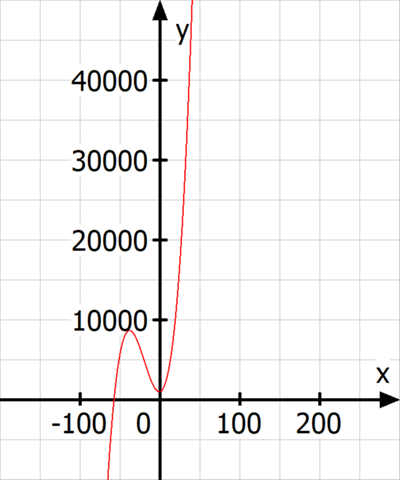
diese Kostenfunktion hat bei etwa x=-38 ein Maximum und bei etwa x=-0,88 ein Minimum.
Vom Minimum an steigt die Funktion kontinuierlich immer steiler an.
Da es schlecht möglich ist, negative Stückzahlen zu produzieren, liegt somit die minimale Kostenzunahme bei der minimal produzierten Stückmenge, die je nach Interpretation 0 oder 1 ist. Bei einer kubischen Funktion wie dieser liegt der Wendepunkt - da er das Symmetriezentrum ist - genau in der Mitte zwischen den Extrema - in diesem Fall also im negativen Bereich; es geht hier einfach nur darum, die Ränder zu überprüfen, hier also den nichtnegativen Bereich der x-Achse.
Herzliche Grüße,
Willy
Du musst die Extrempunkte der Funktionberechnen also K'(x)=0. Wenn es mehrere Lösungen gibt, musst du rausfinden was Minima und was Maxima sind.
Dann K(x) bei den Minima ausrechnen, bei mehreren Minima ist wohl der kleinere Wert die gesuchte Lösung.
Die Funktion sieht momentan so aus:
Kannst du vielleicht noch mal dazu schreiben wie du auf die Kostenfunktion gekommen bist, weil die macht so nocht keinen Sinn zur Aufgabenstellung.
K(x): 0,3x^3+17,5x^2+30x+1000
Eventuell ist deine Kostenfunktion falsch.
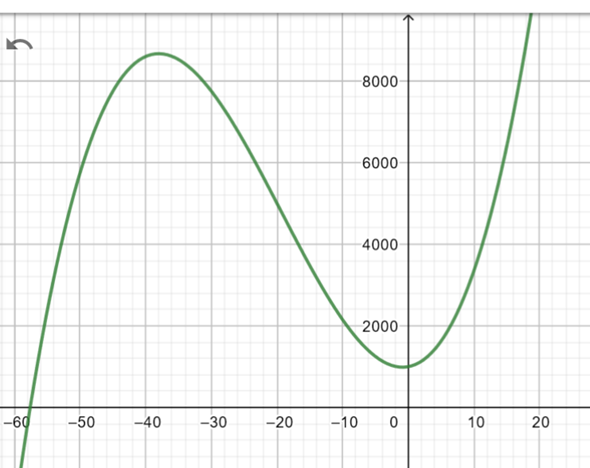
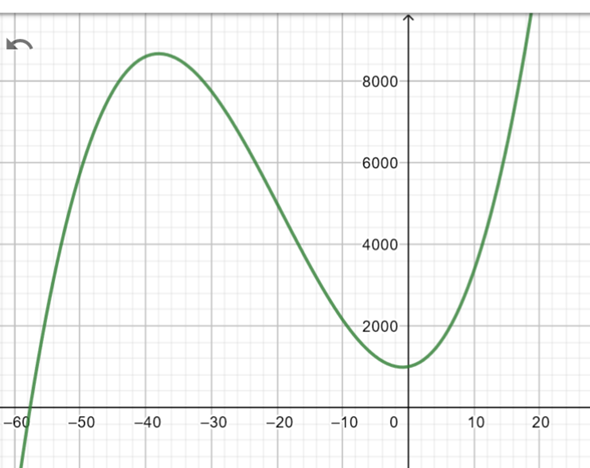
Ich habe der Frage die Aufgabenstellung aus meinem Buch beigefügt und meine Lösung die ich mithilfe meines Taschenrechners herausbekommen habe.
Die Zunahme ist das Gleiche, wie die Steigung der Funktion. Vielleicht kommst du mit der Ableitung weiter.