Bea behauptet:da in jedem parallelogramm die GEGENÜBERLIEGENDEN seiten gleich lang sind,ist jedes parallelogramm ein rechteck,warum stimmt das nicht?
4 Antworten
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Mathematik
Es stimmt zwar, dass auch in Rechtecken gegenüberliegende Seiten gleich lang sind. Aber die Umkehrung stimmt nicht: Nicht jedes Viereck, dessen gegenüberliegende Seiten gleich lang sind, ist ein Rechteck.
Es gibt auch Parallelogramme, die keine Rechtecke sind. Als entsprechendes Gegenbeispiel habe ich ein solches mal skizziert:
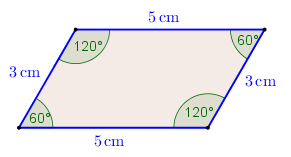
Die Innenwinkel betragen nicht 90°, weshalb es sich nicht um ein Rechteck handelt. Das Viereck ist jedoch ein Parallelogramm.

Ganz einfach, jedes Rechteck und Quadrat ist ein Parallelogramm und Parallelogramme sowieso, aber Rhombus und normales Parallelogram haben keine rechten Winkel!
Nutzer, der sehr aktiv auf gutefrage ist
Ein Parallelogramm hat nicht unbedingt nur rechte Winkel.
Rechtecke haben überall 90°