Aufladen von 2 in Kondensatoren in Serie mit LTspice?
Hallo, zeigt LTspice für die folgende Schaltung falsche Werte für die Spannung an den Kondensatoren?
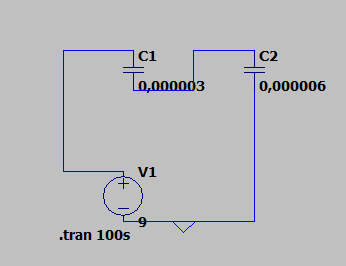
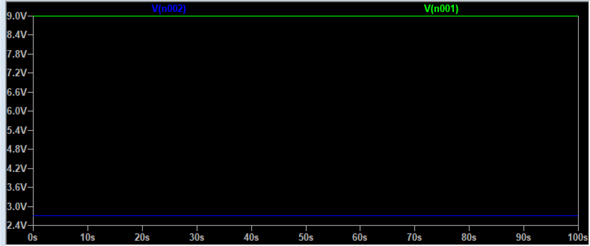
LTspice behauptet am ersten Kondensator fällt eine Spannung von 9V-2,7V=6,3V und am 2. Kondensator dann folglich 2,7V-0V=2,7V ab. So wie ich das aber verstande habe, haben die Spannungsabfälle das gleiche Verhältnis wie die Kapazitäten. Demnach müsste am 1. Kondensator mit 3 Mikrofarad eine Spannung von 6V abfallen und beim 2. Kondensator mit 6 Mikrofarad, 3V. Wer liegt richtig?
4 Antworten
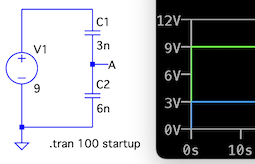
Hänge mal noch ein "startup" an dein Simulationkommando an, dann klappts.
Mit Startup simuliert Spice, dass sowohl die Spannungsquelle am Anfang 0V hat und auch die Kondensatoren leer sind. Man sieht ganz links auch, wie dann die Spannungsquelle "hochgefahren" wird, und dementsprechend sind danach auch die Kondensatoren mit der richtigen Ladung versehen.
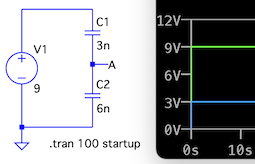
Von der Tendenz her stimmen die Angaben mit deiner Berechnung überein. Woher die 0,3V Differenz kommen, kann man nur wissen, wenn bekannt ist, wie das Programm rechnet.
In der Schaltung sind allerdings keine Werte angegeben.
Das Produkt Q = C * U ist die Ladung auf dem Kondensator C bei der Spannung U.
Da die Ladung bei beiden Kondensatoren gleich ist, sind Spannung und Kapazität umgekehrt proportional.
Ich schätze mal, dass die Ergebnisse anders ausfallen, wenn Du eine DC-Analyse machst, oder bei der TRAN-Analyse eine andere Auflösung wählst.
Warum? Weil das hier das klassische Zwei-Kondensator-Problem ist. In der Praxis werden sich beide Kondensatoren nämlich in Abhängigkeit der Verlustwiderstände (Leckströme) aufladen - unabhängig von den C-Werten. Das gilt natürlich nur für Gleichspannung - bei Wechselspannung gilt normal Xc=1/wC.
Ich weiß jetzt nicht, ob die C-Modelle bei LTSpice evtl. so einen Verlust-Widerstand schon beinhalten.
Zwei IDEALE Kapazitäten verhalten sich bei Gleichspannung jedenfalls nicht gemäß Q=C*U, weil sie sich in unendlich kurzer Zeit aufladen müssten, was nicht geht.
Fazit: Die Ergebnisse sind unbrauchbar, weil willkürlich.