Ableitung von Wurzel(e^x)?
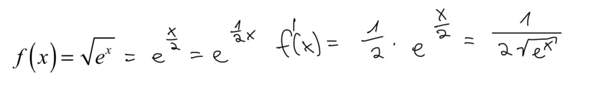
Hi, mein Lehrer und ich haben unterschiedliche Lösungen.
Er gibt an: f(x)=Wurzel(e^x) f‘(x)=1/(2•Wurzel(e^x)) • e^x
Ich meine aber, laut Kettenregel:
f‘(x)= 1/(2•Wurzel(e^x)) // ohne mal e^x
Die kettenregel geht doch so: u‘(v(x)) • v‘(x) ,oder?
Wäre dankbar für einen Rechenweg mit Begründung. Lg
Wie kommt in der handschriftlichen ersten Zeile am Ende Wurzel x in den Nenner?
Rechenfehler, danke dir. Die Wurzel x müsste in den Zähler, also Wurzel(e^x)/2
2 Antworten
Hi,
die Ableitung ist:
Die Erklärung erfolgt, wie du sagst, über die Kettenregel.
f(x) = Wurzel(e^x) = (e^x)^(1/2) = e^(1/2 x)
u(x) = e^x => u'(x) = e^x
v(x) = 1/2x => v'(x) = 1/2
Kettenregel ergibt:
LG
Gern Geschehen. :)
Und nein, das kann nicht sein. Denn 1(2*W(e^x)) = 1/2 * e^(-x/2). Und wir haben hier ja e^(x/2) ohne ein Minus. Deshalb darf die Wurzel nicht in den Nenner.
Edit: Sehe gerade dass du die Wurzel aus Versehen in den Nenner geschrieben hast. Wenn der Lehrer die in den Zähler gepackt hat, stimmen unsere Terme natürlich überein :)
Dein Lehrer hat natürlich recht weil die Anleitung von e^x eben e^x ist
Schon klar dass mein Lehrer recht hat, er hat Mathe studiert. Ich hätte aber gerne einen Rechenweg, damit ich es verstehe. Du bist mir keine Hilfe…
Doch ich habe dir gesagt wo dein Fehler ist.
Aber noch einfacher für dich du kannst es als (e^x)^0.5 schreiben, dann ist u’ eben 0.5*(e^x)^-0.5 und v’=e^x
das mit dem Studieren hilft nicht immer, eine Matheprof bei uns meinte immer, sagt a, schreibt b, denkt c und d wäre richtig
ich Gebe lieber Tipps als fertig Lösungen zum
abschreiben, das ist besser zum
verstehen
Wenn man Wurzel x umschreibt, hat man x^(1/2). Ohne Minus. Da scheint auch der Fehler in der Lösung oben zu stecken. Wenn das Minus da wäre, muss natürlich die Wurzel in den Nenner wandern. Aber das ist hier nicht der Fall.
Wenn du 1/2*Wurzel(e^x) hast, dann heißt das, dass die Wurzel(e^x) zum Zähler gezählt wird, nicht zum Nenner. Das ist der einzige Denkfehler :)
wurzel ist hoch 0.5 in der Ableitung dann 0.5 mal hoch -0.5
Achtung: Kettenregel! Du kannst das nicht einfach nach der Potenzregel ableiten, da du e^x mit drin hast 😅 zwar ist Wurzel hoch 0,5 aber du hast ja e^(0,5x). Du musst das in e^x und in 0,5x aufteilen, und dann die Verkettung der Funktionen mit der Kettenregel ableiten. Vielleicht siehst du jetzt, dass du falsch liegst.
Potenzrechenregeln sind das Zauberwort, stimmt. Es ist ja letztlich e^.5x - du hast also recht
In dem Fall wären aber sowohl deine als auch die Ableitung von meinem Leher richtig. Laut GeoGebra sind beide Terme die gleiche Konstante. Frage mich nicht warum, das hat mich die ganze Zeit verwirrt.