zwei e-Funktionen gleichsetzen?
Habe folgende Gleichungen:
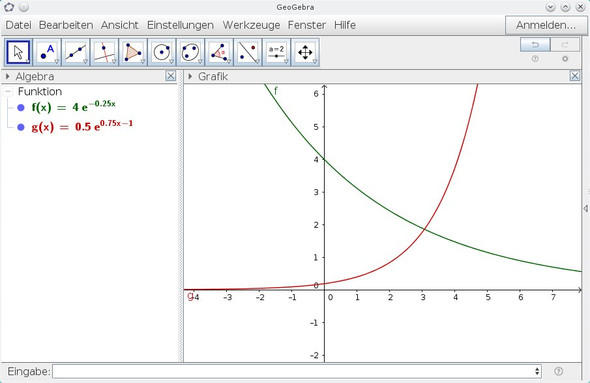
f(x)=4e^(-0,25x) und g(x)=0,5e^(0,75x-1)
ich muss den Schnittpunkt finden :(
Vergesse trotz meiner 14 Punkte (Note: 1) in Mathe halt trotzdem manchmal Grundlagen und da hoffe ich, das mir hier jemand helfen kann :)
Oliver
3 Antworten
durch 0,5 teilen
8e^-0,25x = e^(0,75x-1) ln
ln8 -0,25x = 0,75x-1 nach x auflösen
x = 3,079
Hallo daFreac,
Funktionen gleichsetzen. Alle e-Funktionen auf die linke Seite, alles andere auf die rechte. Potenzregeln anwenden ergibt:
e^(x-1) = 8
Logarithmieren: Schnittpunkt ist x = 1+ln 8
Gruß von leiermann
MERKE: Steht x im Exponenten,dann immer "Potenzgesetze","Logarithmengesetze" und "Substitution" anwenden
e^-1=1/e^1=1/e
4*e^(-0,25*x)=0,5*e^(0,75*x-1)=0,5*e^(0,75*x)*e^-1 ergibt
e^(-0,25*x)/e^(0,75*x=0,5/4 *1/e^1=K
siehe Mathe-Formelbuch Potenzgesetze a^r/a^s=a^(r-s)
e^(-1*x)=K Substitution z=-1*x
e^z=K logarithmiert ergibt z=ln(K)=-3,079 mit z=-x ist x=3,079