zahlenfolge 0 6 12 24 48 ... term
hallo,
ich habe vor kurzem in der schule die aufgabe bekommen für die oben genannte zahlenfolge einen term zu berechen bei welchem man durch einsetzen von den zahlen 1,2,3,4 ... das ergebnis bekommmt: also das bedeuted wenn man bei dem term die variable 1 einsetzt 6 bekommt, bei 2 12, bei 3 24,bei 4 48 usw.
brauche den term dafür!
danke schonmal im vorraus alex
5 Antworten
Wenn du durch 6 teilst, kriegst du 0, 1, 2, 4, 8, etc. Versuch das mal als Term darzustellen.
Gleichgung:
f(x) = x^3-6x^2+17x-12
Dann ist:
f(1) = 0
f(2) = 6
f(3) = 12
f(4) = 24
f(5) = 48
Das ist doch, was du meintest, oder?
Du hast es ja selbst missverständlich in den Titel geschrieben.
stimmt nächstes mal drücke ich mich klarer aus :D
das ist genau meine Polynomfunktion verschoben um 1,denn x(12+(x-4) (x+1)) = 8x - 3x² + x³
Das ist wieder so eine Folge ohne Randbedingungen -> also mit unendlich vielen Lösungen:
§1 per Polynomanalyse (www.gerdlamprecht.de/Mittelwerte.html) liefert:
x * 8-pow(x,2) * 3+pow(x,3) = 8x - 3x² + x³
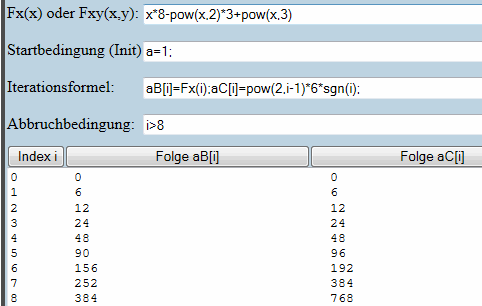
§2 tinafritz1992 kombiniert mit der sgn-Funktion siehe Bild vom Iterationsrechner
§3 3/49= 0.06 12 24 48 97 95 91 83 67... also je 2 Nachkommastellen
§4 A160728 = 0, 6, 12, 24, 48, 72, 96, 120, 144,... siehe OEIS
...
noch mehr Lösungen -> erst wenn es Randbedingungen (Einschränkungen) gibt.
Als Zugabe noch 2 schöne weiche ohne Knicke:
§5:
aB[i]=(pow(i,3) * 30-pow(i,4) * 3-pow(i,2) * 85+90 * i+88) * i/20; ergibt
0, 6, 12, 24, 48, 72, 48, -126, -624,....
§6: aC[i]=((i+4) * Fx(i)+2 * i * Fx(i-1)) * 6/5; mit den Fibonacci-Zahlen Fx(x)=pow(sqrt(5) * 0.5+0.5,x)/sqrt(5)+pow(sqrt(5) * 0.5-0.5,x) * sin(PI*(x-0.5))/sqrt(5) ergibt
0, 6, 12, 24, 48, 90, 168, 306,...
n=1 => 1 * 6 = 2^0 * 6
n=2 => 2 * 6 = 2^1 * 6
n=3 => 4 * 6 = 2^2 * 6
Jetzt sieh dir mal den Zusammenhang zwischen n und den Potenzen an!
Kleiner Tipp: du kannst auch noch die 6 in 2 * 3 zerlegen und die 2 dann zu den Potenzen hinzu fügen. Da freut sich dein Lehrer!
Das erste stimmt nicht, da 2^0=1 -> kann aber durch Multiplikation mit der sgn(x) Funktion "hingebogen" werden, da sgn(0)=0 else 1
-> siehe Bild
Soll laut Aufgabe: f(0)=0
Dein pow(2,n-1) * 6 liefert bei n=0
pow(2,-1) * 6 = 1/ 2 * 6 =3
und das kann mit der Multiplikation per sgn(x) korrigiert werden, denn sie liefert nur bei Argument 0 eine 0 ansonsten eine 1...
schau Dir einfach das Bild an...
Jetzt verstanden?
Wollte Dir doch nur helfen die auch richtige Idee ab n=1 in die absolut richtige explizite Form ab n (bzw. x) = 0 zu erweitern.
eine andere Möglichkeit für f(0)=0 zu bekommen und dabei die sgn Funktion nicht zu benutzen ist per floor(x) "Abrunden": floor(pow(2,i-1))*6
denn floor(1/2)=0
Wenn du jeden Wert durch 6 teilst, fällt dir nichts auf?
ich meine ich brauche einen term. wenn ich dann z.B. die variable n durch 3 ersetze soll 24 raus kommen aber wenn ich im selben term n durch 1 ersetze soll 6 raus kommen.
das stimmt nicht denn bei f (1) muss 6 raus kommen trotzdem danke!