Winkel zwischen 2 Punkten mit xy Koordinaten berechnen?
Hallo,
zunächst sorry für den Doppelpost, ich habe es nicht hinbekommen, nachträglich ein Bild einzufügen.
ich würde gern in Javascript eine Art Tangram Spiel programmieren.
Dazu muss ich unter anderem verschiedene Punkte um andere Punkte drehen.
Das funktioniert auch sehr gut mit folgenden Berechnungen. Dabei ist (x0, y0) der Punkt, um den der Punkt (x1, y1) gedreht werden soll:
x = x0 + (x1 - x0) * cos(winkel) - (y1 - y0) * sin(winkel)
y = y0 + (x1 - x0) * sin(winkel) + (y1 - y0) * cos(winkel)
Allerdings müsste ich zuvor den Winkel berechnen, um den gedreht werden soll.
Folgende Formel habe ich im Internet dazu gefunden:
winkel = arctan((y2 - y1) / (x2 - x1))
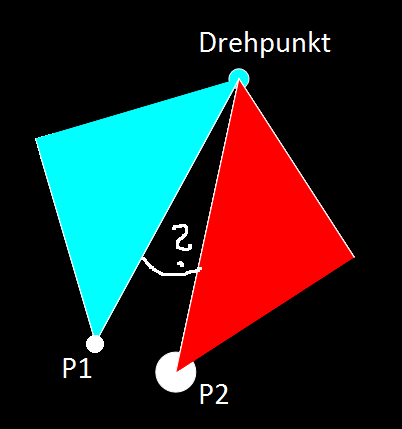
Allerdings wird hier ja nicht der Drehpunkt aus dem Bild berücksichtigt, weshalb leider nicht der Winkel berechnet wird, den ich benötige.
Kann mir jemand auf die Sprünge helfen?
Gern auch mit einer fertigen Formel.
Vielen Dank und beste Grüße
Christoph
4 Antworten
Mit D bezeichne ich den Drehpunkt. Mit v bezeichne ich den Vektor von D nach P1. Mit w bezeichne ich den Vektor von D nach P2. Dann berechnet sich der Winkel alpha zwischen v und w vermöge
Ein Punkt, den du mithilfe von Koordinaten angibst, IST ein Vektor. Sagen wir,
D = (x0,y0)
P1 = (x1,y1)
P2 = (x2,y2)
Dann ist v = (x1-x0,y1-y0) und w = (x2-x0,y2-y0).
Oder auch kurz: v = P1 - D und w = P2 - D.
Das Skalarprodukt ist dann
v * w = (x1 - x0) * (x2 - x0) + (y1 - y0) * (y2 - y0).
Die Länge von v ist
|v| = sqrt((x1 - x0)² + (y1-y0)²). Entsprechendes gilt für |w|.
Damit kannst du wie oben angegeben cos(alpha) berechnen. Wirfst du jetzt arccos auf das Ergebnis, erhältst du deinen Winkel.
Wenn es dir nicht passieren kann, dass zwei x-Koordinaten gleich sind, ist der Weg von gfntom aber wohl angenehmer.
Mit den 2D-Koordinaten P1, P2 und D (vom Drehpunkt) gilt für den ?-Winkel alpha (unter Verwendung des Skalarprodukts und des Betrags):
(P1 - D)(P2 - D )/(|P1 - D||P2 - D|) = cos(alpha)
Jetzt brauchst Du also nur noch die Arccos-Funktion.
Das sieht auch gut aus, vielen Dank für die Antwort.
Probiere ich aus.
Auch hier nochmal:
Du willst nicht den Winkel zwischen zwei Punkten berechnen, sondern zuwischen zwei Geraden, und zwar zwischen den Geraden D_P1 und D_P2. D bezeichnet hier den Drehpunkt.
Die Formel passt schon, du musst sie nur 2 mal anwenden und die Ergebnisse subtrahieren. Einmal berechnest du den Winkel zwischen der Geraden D_P1 und der Horizontalen, und einmal der Winkel zwischen D_P2 und der Horizontalen.
Oh, das klingt äußerst sinnvoll, vielen Dank für deine Antwort.
Das probiere ich gleich aus.
Vielen Dank, genau das war das Problem.
Meine Frage ist damit beantwortet.
Du betrachtest zunächst die Vektoren S1:=P1-Drehpunkt und S2:=P2-Drehtpunkt, d.h. du gehst einfach davon aus, dass der Drehpunkt 0 ist. Dann brauchst du nur noch den Kosinussatz
Danke für deine Antwort.
Leider kann ich mit der Schreibweise S1:=P1-Drehpunkt nicht viel anfangen. Was ist damit gemeint?
Danke für deine Antwort.
Ich würde gern mit den vorhandenen x und y Koordinaten rechnen.
Gibt es eine Lösung ohne Vektoren?