Wie rechnet man hier den Winkel phi aus?
Ich habe bis jetzt nur herausgefunden wie man ihn cos positiv ausrechnet aber so? Muss man einfach sin(alpha) ausrechnen? Aber habe ich da nicht den Winkel innerhalb des rechtw. Dreiecks?
1 Antwort
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Mathematik
Ich gebe Regeln an, für die du einen positiv orientierten Winkel α mit 0° < α < 360° herausfindest, für den
- die x-Achse einen Schenkel bildet und
- die Verlängerung des "Zeigers" im Einheitskreis die den zweiten Schenkel bildet,
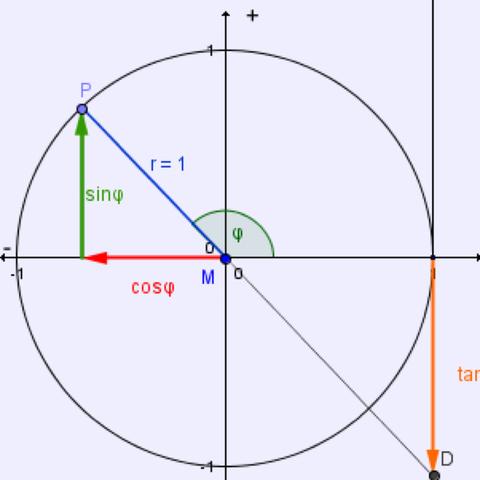
also so, wie das auf dem Bild der Fall ist (nur allgemeiner).
Möglichkeit 1: Der Sinus des Winkels ist gegeben.
- Dann rechnest du mit arcsin (auf dem Taschenrechner. "sin hoch minus 1") einen Winkel aus, der diesen Sinus hat.
- Die arcsin-Funktion gibt immer einen Winkel α an, für den gilt: -90° ≤ α ≤ + 90°.
- Für Winkel, bei denen der "Zeiger" im Einheitskreis sich im ersten Quadranten befindet, ist dann α der gesuchte Winkel.
- Für Winkel, bei denen der "Zeiger" im Einheitskreis sich im vierten Quadranten befindet, ist dann 360° + α der gesuchte Winkel, denn der hat den gleichen Sinus wie α.
- Für Winkel, bei denen der "Zeiger" im Einheitskreis sich im zweiten oder dritten Quadranten befindet (wie hier, der Zeiger ist im zweiten Quadranten), ist dann 180° - α der gesuchte Winkel, denn der hat den gleichen Sinus wie α.
Möglichkeit 2: Der Kosinus des Winkels ist gegeben.
- Dann rechnest du mit arccos (auf dem Taschenrechner. "cos hoch minus 1") einen Winkel aus, der diesen Kosinus hat.
- Die arccos-Funktion gibt immer einen Winkel α an, für den gilt: 0 ≤ α ≤ 180°.
- Für Winkel, bei denen der "Zeiger" im Einheitskreis sich im ersten oder im zweiten Quadranten befindet (wie hier, der Zeiger ist im zweiten Quadranten) ist dann α der gesuchte Winkel.
- Für Winkel, bei denen der "Zeiger" im Einheitskreis sich im dritten oder vierten Quadranten befindet, ist dann 360° - α der gesuchte Winkel, denn der hat den gleichen Kosinus wie α.
Möglichkeit 3: Der Tangens des Winkels ist gegeben.
- Dann rechnest du mit arctan (auf dem Taschenrechner. "tan hoch minus 1") einen Winkel aus, der diesen Tangens hat.
- Die arctan-Funktion gibt immer einen Winkel α an, für den gilt: -90° ≤ α ≤ + 90°.
- Für Winkel, bei denen der "Zeiger" im Einheitskreis sich im ersten Quadranten befindet, ist dann α der gesuchte Winkel.
- Für Winkel, bei denen der "Zeiger" im Einheitskreis sich im vierten Quadranten befindet, ist dann 360° + α der gesuchte Winkel, denn der hat den gleichen Tangens wie α.
- Für Winkel, bei denen der "Zeiger" im Einheitskreis sich im zweiten oder dritten Quadranten befindet (wie hier, der Zeiger ist im zweiten Quadranten), ist dann 180° + α der gesuchte Winkel, denn der hat den gleichen Tangens wie α.
Möglichkeit 4: Der Kotangens des Winkels ist gegeben.
- Dann rechnest du mit arccot (auf dem Taschenrechner. "cot hoch minus 1") einen Winkel aus, der diesen Kotangens hat.
- Die arccot-Funktion gibt immer einen Winkel α an, für den gilt: 0 ≤ α ≤ 180°.
- Für Winkel, bei denen der "Zeiger" im Einheitskreis sich im ersten oder im zweiten Quadranten befindet (wie hier, der Zeiger ist im zweiten Quadranten) ist dann α der gesuchte Winkel.
- Für Winkel, bei denen der "Zeiger" im Einheitskreis sich im dritten oder vierten Quadranten befindet, ist dann 180° + α der gesuchte Winkel, denn der hat den gleichen Kotangens wie α.