Wie rechne ich den Limes aus?

Hallo Leute,

also es geht um die Aufgabe 5). Ich weiß nicht so ganz wie ich das jetzt ausrechnen soll und wie man auf das Ergebnis kommt. Klar ist, dass ich jetzt für n unendlich einsetzen muss. Da würde unendlich hoch 4 durch unendlich hoch 3 plus 1 reinkommen. Aber was hat das dann für einen Sinn? Ich bedanke mich schonmal im Voraus ^^

Answer 1

[PWolff]

Man kann in solchen Fällen versuchen, den Ausdruck auf einen Ausdruck einer der Formen

1 + O(1/n)

n^a + O(n^(a-1))

n^(-a) + O(n^(-a-1))

(a > 0) zu bringen; dann kann man den Limes sofort ablesen (und auch das "asymptotische Verhalten").

In diesem Fall

$\frac{n^4}{\left(n^3+1\right)}=\frac{\left(n\ n^3\right)}{\left(n^3+1\right)}=\frac{\left(n\ \left(n^3+1-1\right)\right)}{\left(n^3+1\right)}=n\ \frac{\left(n^3+1\right)}{\left(n^3+1\right)}-\frac{n}{\left(n^3+1\right)}=n-\frac{n}{\left(n^3+1\right)}$

Ich denke, ihr könnt schon voraussetzen, dass der Subtrahend gegen 0 geht für n gegen unendlich, sonst könnte man hier z. B. ebenfalls im Zähler eine "nahrhafte 0" addieren, in diesem Fall

$+\frac{1}{n^2}-\frac{1}{n^2}$

Dann haben wir einen Summanden, der für n gegen unendlich ebenfalls gegen unendlich geht, und einen oder mehrere Summanden, die für n gegen unendlich beschränkt bleiben oder gegen 0 gehen.

-----

Man kann die Pseudo-Zahlen "unendlich" (ohne definiertes Vorzeichen), "+unendlich" und "-unendlich" einführen und konsistente Rechenregeln definieren, aber ich glaube nicht, dass das bei euch akzeptiert wird. Außerdem ist

unendlich^4 = unendlich,

unendlich^3 = unendlich

und

unendlich / unendlich

nicht sinnvoll definierbar, sodass man dann schon auf die Landau-Symbole zurückgreifen müsste. Aber auch diese müssen erst einmal definiert sein.

Answer 2

[LORDderANALYSE]

Logik

Wir betrachten die Funktionen einfach einzeln...

Regel von L'Hospital

Sowohl Nenner als auch Zähler divergieren gegen +unendlich. aka wir können die Regel von L'Hospital anwenden aka wir leiten b und versuchen dort das gleiche mit Limes. Das dauert hier jedoch.

Erweitern

(siehe Antwort von TBDRM)

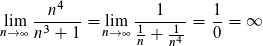
(eigetnlich +unendlich und -unendlich, doch nur +unendlich ist korrekt)

Plotten

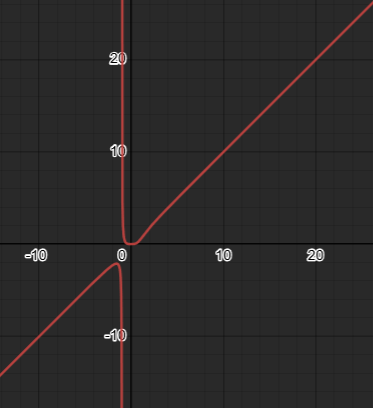
Gegen was geht wohl y bei x gegen unendlich?
Unendlich!

Funktionstheorie

• die Funktion ist für alle positiven x stetig (aka keine Lücken)
• die Funktion hat ein Minimum und ein Maximum, wobei das letzte Extrema ein Maximum ist, also geht es danach nur noch nach oben, also in unendliche, wenn die Funktion in diesen Intervall stetig ist

Doch das ist sie ja, also geht die Funktion für x gegen unendlich selbst gegen unendlich.

Woher ich das weiß: Studium / Ausbildung

Answer 3

[TBDRM]

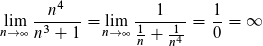
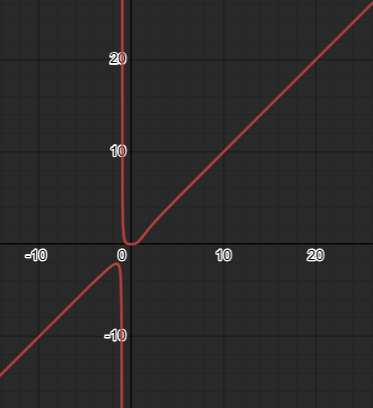
Bruch erweitern mit 1/x⁴

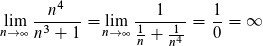
Das passt auch zum Graphen. Je weiter man nach rechts (ins Unendliche) geht, desto höher steigen die Werte (also auch ins Unendliche):

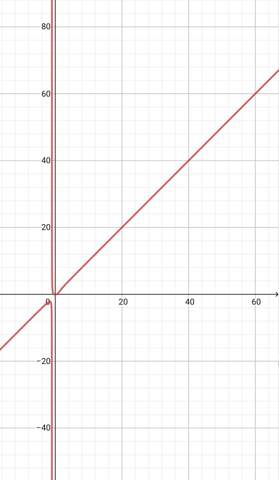
Ich hoffe, ich konnte helfen :)

Woher ich das weiß: Hobby – Mathematik (u. Physik)

Comments

[Saskal]

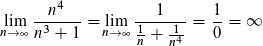
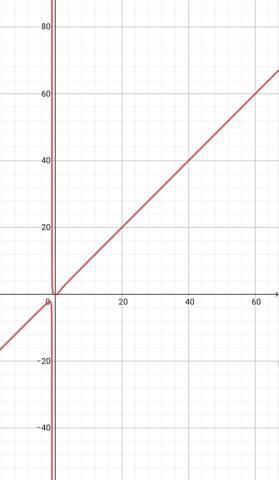
Und woher weiß man dass man 1 durch x hoch 4 rechnen muss?

[TBDRM]

@Saskal

Übung