Wie konstruiere ich die Tangente mit nur 3 Linien (Geometrierätsel)?
Ich muss an diesem Punkt die Tangente konstruieren.
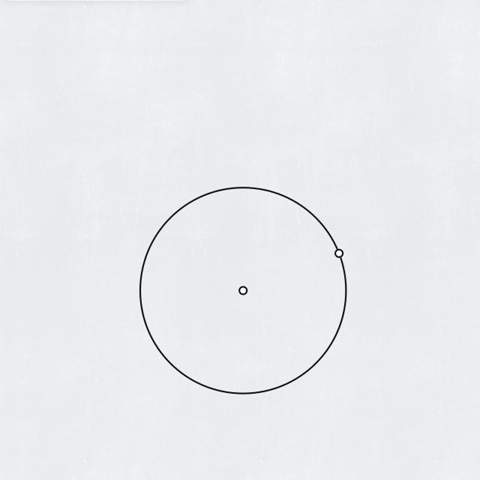
Ich habe bereits 2 Möglichkeiten gefunden, diese benötigen allerdings entweder 3 Kreise und eine Linie oder 2 Kreise und 2 Linien:


Anscheinend soll es aber möglich sein die Tangente mit 2 Kreisen und einer Linie (in der Abfolge) zu konstruieren. Ich komme aber einfach nicht drauf wie man das machen könnte... (Vielleicht bin ich auch einfach grade zu blöd und übersehe das offensichtliche...)
Habt ihr vielleicht eine Lösung oder könnt ihr mir Tips geben wie ich das noch versuchen kann?
Hier noch ein Möglichkeit mit 3 Kreisen und 2 Linien:

Und hier ein paar Sachen, die noch nicht funktionieren:

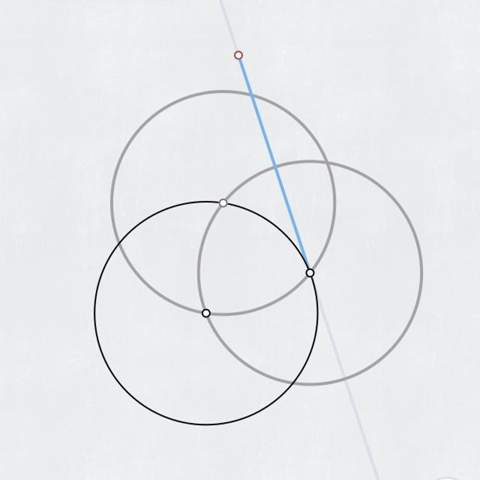
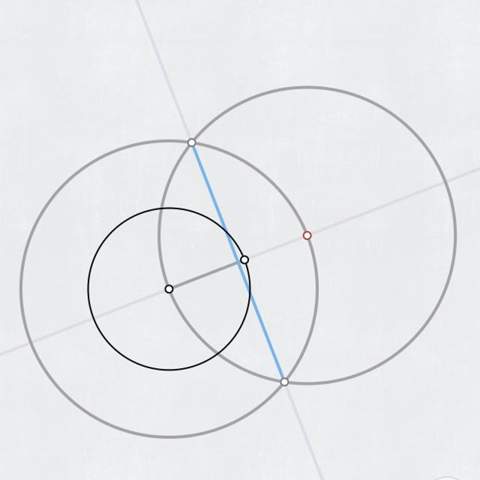
Und hier eine Tangente mit 2 Kreisen und einer Geraden an der falschen Stelle XD
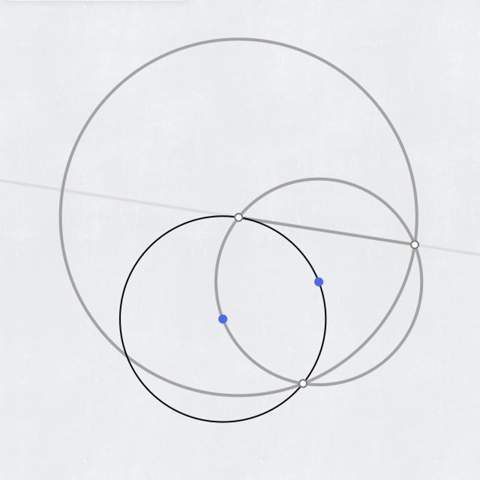
Ok, danke für alle, die versucht haben zu helfen. Ich habe die Lösung gefunden falls es jemanden interessiert:

5 Antworten
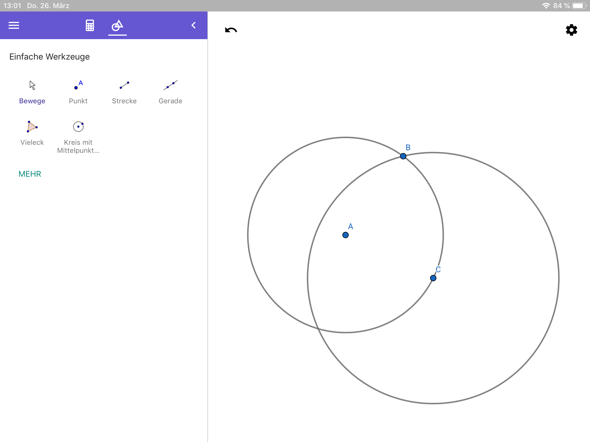
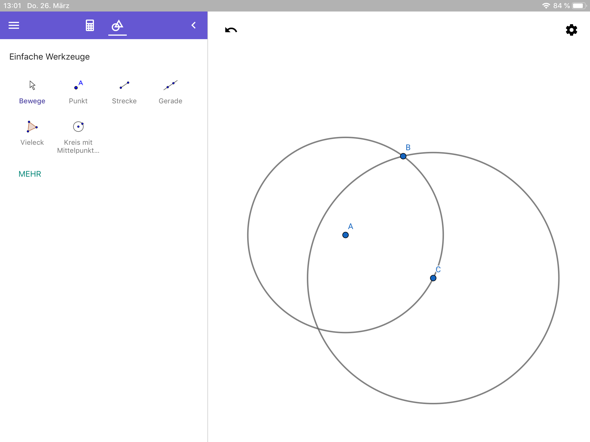
Hi, ich habe eine Lösung gefunden! Kreis mit dem Mittelpunkt A und einem Punkt B, durch den die Tangente laufen soll.
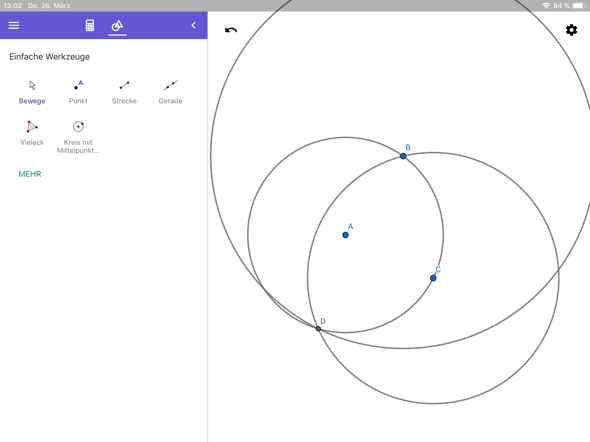
- Irgendeinen Punkt C auf dem Kreis nehmen und einen 2. Kreis mit dem Radius CB zeichnen:
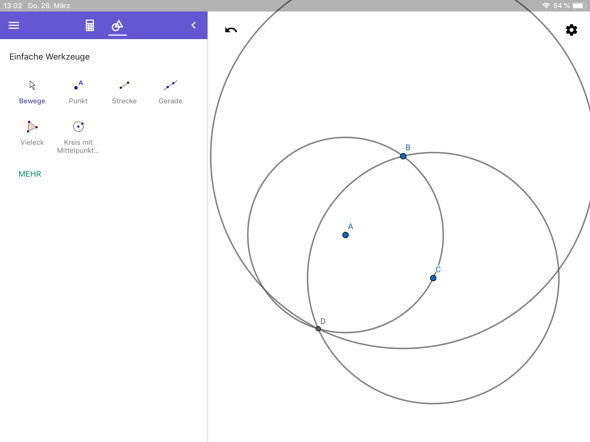
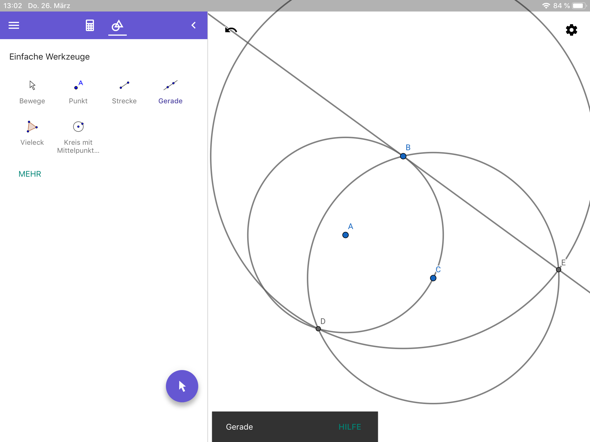
2. Den Schnittpunkt der Kreise D nennen und einen Kreis um B mit dem Radius BD zeichnen. Die Tangente ist jetzt die Verbindung von B und dem Schnittpunkt der beiden neu gezeichneten Kreise.
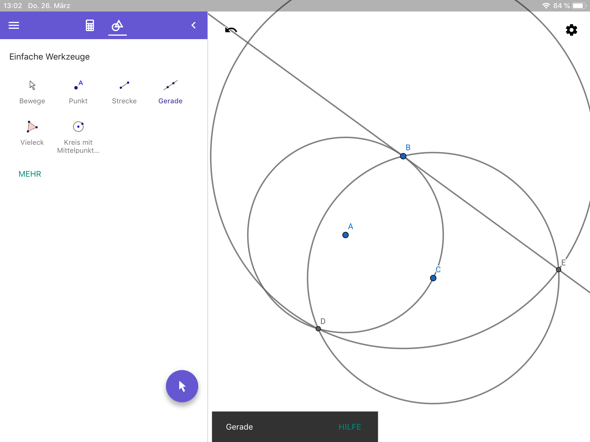
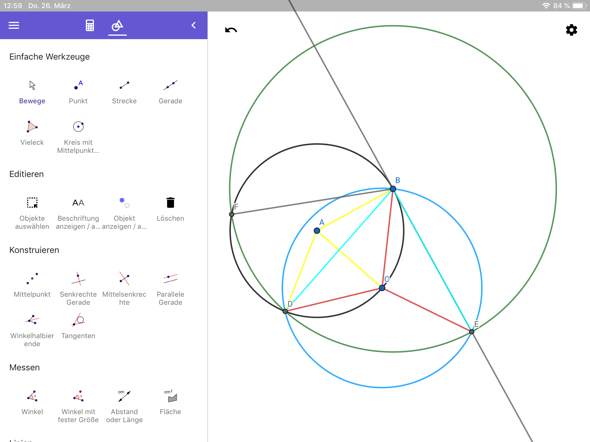
Warum funktioniert das? Ich habe mal die gleich langen Strecken mit der gleichen Farbe markiert, sie sind dann immer Radien im gleichen Kreis.
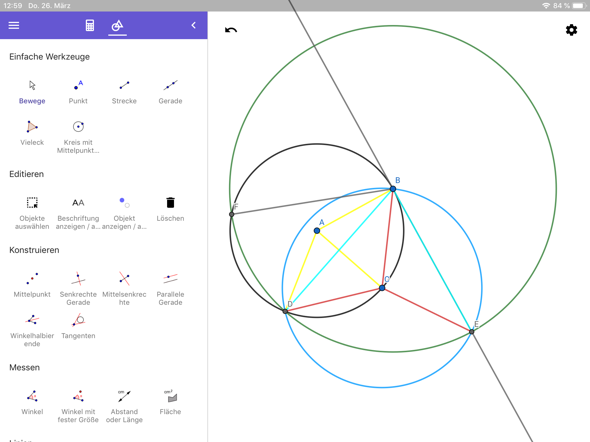
Die Winkel bezeichne ich jetzt mit den beiden Seiten die sich schneiden, also der Winkel ABC ist der Winkel „gelbrot“. Da die Dreiecke ADC und BAC kongruent sind gilt: für den großen Winkel bei C:
rotrot = 2 gelbrot
Außerdem gilt für die Innenwinkelsumme im Dreieck BCE:
180 grad = rotrot + 2 blaurot
Aus den beiden Gleichungen entsteht:
90 grad = gelbrot + blaurot
Dies ist der Winkel zwischen dem Radius des ursprünglichen Kreises und der mutmaßlichen Tangente. Es ist also wirklich eine Tangente. QED
Die Beweise, dass alle Winkel mit dem gleichen Namen gleich groß sind aufgrund von Kongruenz fehlen natürlich, aber das ist ja logisch.
Ich saß länger als ne Stunde an der Frage... :D
Ich habs auch beim rumspielen entdeckt und dann versucht einen Beweis zu finden. Das mit der Zeit ist kein Problem, weil ich den ganzen Tag über Mathe machen könnte ohne dass mir langweilig wird :) Deshalb hab ich auch erst am Ende gemerkt wie lange das eigentlich gedauert hat... :D
Was spricht dagegen, den Kreismittelpunkt mit dem Radius zu verbinden und im Radius eine Normale drauf zu setzen?
oder habe ich etwas nicht verstanden?
(mir ist so, als sähe man es auf den ersten Blick und das ist oft eine Falle)
Die Normale muss vermutlich konstruiert werden und nicht einfach "gemessen"
jetzt fühle ich mich provoziert und habe mir das aufgezeichnet. Was ist damit:
(leider habe ich seit 30 Jahren keinen Zirkel mehr benutzt):
Ich steche in den Umfang ein, messe bis zum Mittelpunkt und finde damit den Radius, den ich nach außen hin auftrage. Damit zeichne ich drei ineinander verschlungene Kreise. Ich hoffe, ich kann hier meine Grafik einfügen.
Ich kann leider bei dem Rätsel keine rechten Winkel abmessen und müsste das ganze dann wieder mit mehreren Kreisen konstruieren. Dann bräuchte ich sogar 3 Kreise und 2 Linien.
mein neues Bild ist gezeichnet, ich muss es nur noch verlinken
https://abload.de/image.php?img=kreiselbjrw.png
bitte probiere, ob das geht, wie gesagt, ich habe keinen Zirkel.
nicht zu "irgendwie". Sondern die Kreise haben den Radius des ersten Kreises. Du stichst in den Umfang ein und misst bis zum Mittelpunkt.
Durch die Schnittpunkte kannst Du dann Deine Tangente parallel-verschieben. Der erste Kreis ist schon da, damit zeichnest Du nur 2 neue.
“gleicher Radius“ geht nicht. Entweder ich habe einen Referenzpunkt oder der Kreis hat eine beliebige Größe.
Und ich verstehe nicht was du mit „parallelverschieben“ meinst. So weit ich weiß kann man das bei dem Rätsel nicht.
So hätte ich dann zwar 2 Kreise, die helfen aber nicht weiter...
Ich kann leider nichts verschieben deswegen ist das wohl auch nicht möglich. Und Dreiecke habe ich auch nicht zur Verfügung.
Ich kann nur geraden zwischen 2 Punkten setzen und Kreise ziehen, die von einem Mittelpunkt zu einen Radius-punkt gehen. Notfalls kann ich auch beliebig irgendwelche Punkte setzen aber das bringt nicht sehr viel. Die Lösung soll „exakt“ sein und für jede mögliche Position der vorgegebenen Punkte gelten. Also sollten am besten alle neuen Punkte über Kreise und Geraden an den Ursprungspunkten verankert sein.
wie wäre es damit:
- Du stichst in den Umfang ein und zeichnest einen neuen Kreis mit dem Radius des Umfangs. D.h. Du hast danach den kleinen Angabe-Kreis im Innenbereich des großen. NICHT konzentrisch.
- jetzt zeichnest Du einen zweiten Kreis mit dem Mittelpunkt auf dem großen Kreis und dem 1,5 Fachen des Umfangs
- durch die Schnittpunkte legst Du die Tangente
Du kannst so mit zwei Kreisen und einer Linie eine Tangente an beiden Kreisen erstellen

Also den einen Kreis auf dem Rand des anderen Kreisen zeichnen und dann einfach eine Gerade suchen, die beide Ränder verbinden kann

Nur habe ich den Einstech-punkt für den 2. Kreis nicht gegeben. Den müsste ich erst aufwendig konstruieren.
Wieso denn? Du kannst den irgendwo auf dem anderen Kreis erstellen! Das ist dann doch dasselbe nur, dass der zweite Kreis dann evtl höher oder niedriger liegt
Sorry, hab überlesen/übersehen, dass Du die Tangente an einem bestimmten Punkt konstruieren sollst. My bad :(
Aber dann habe einen Kreis für irgendeine Tangente und nicht mehr für den gesuchten Punkt. Außerdem muss ich auch noch herausfinden wo auf meinem 2. Kreis die Linie durchgehen muss.
Aber schau mal, bei deiner Ergänzung kannst du doch den zweiten inneren Kreis weglassen oder nicht? Wenn du die Linie vom mittelpunkt des originalkreises durch den tangentenpunkt verlängerst kommst du doch auch auf den Mittelpunkt für den zweiten großen Kreis rechts?
Nein, wenn ich dich jetzt gerade richtig verstehe würde das so nicht funktionieren. Um den Mittelpunkt des großen Kreises rechts oben herauszufinden brauche ich den Abstand auf der Linie zwischen Mittelpunkt und Tangentenpunkt. Dafür verwende ich den kleinen Kreis. Weglassen kann ich da also glaube ich nichts.
Was ist denn erlaubt?
Der rechte Winkel muss vermutlich konstriert werden, oder?
Parallelverschieben? Wenn erlaubt: Kreis mit Mittelpunkt Berührpunkt und Radius des ursprünglichen Kreises. Schnittpunkte verbinden. Parallelverschieben
Parallelverschieben geht nicht. Es gibt nur Kreise und Geraden. Und die sollte man an Schnittstellen oder vorgegebenen Punkten verankern.
Möglicherweis ist gemeint "Zwei Kreise und eine Linie als Hilfsobjekte vor dem Einzeichnen der Tangente"?
Nein, leider nicht. Sonst müssten ja meine bisherigen Lösungen funktionieren...
Danke, ich hab das grad beim rumspielen auch gefunden aber überhaupt nicht verstanden wie das funktioniert. Das ist ja richtig genial ^^
Und tut mir leid, dass du jetzt so viel Zeit damit verbracht hast das ist mega nett, danke :)