Wie kommt man hier auf die Ebenengleichung?
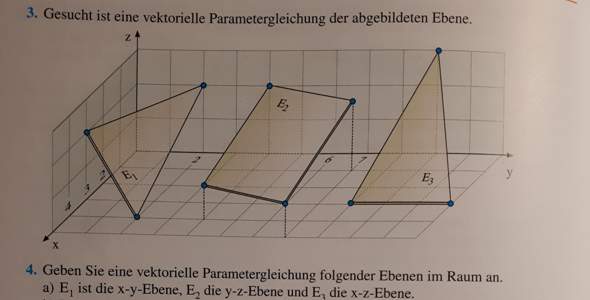
Aufgabe 4a) verstehe irgendwie nicht ganz was da gemeint ist, kann jemand weiterhelfen?
2 Antworten
x-y-Ebene → alle Punkte z=0 Ebene hat den Punkt A(0/0/0)
die Richtungsvektoren kannst du nun frei wählen
u(ux/uy/uz)=u(1/1/0) → z=0 weil alle Ebenenpunkte z=0 haben
v(vx/vy/vz)=v(1/2/0)
Infos


Du nimmst deinen Schreibtisch als x-y-z-Koordinatensystem
linke Tischkante ist die x-Achse
vordere Tischkante ist die y-Achse
einen Bleistift,den du senkrecht auf die linke vordere Tischecke stellst,ist die z-Achse
a) z-Komponente aller Punkte der x-y-Ebene z=0
Die Ebene ist somit die Tischoberfläche und der Punkt P(0/0/0) (Ursprung) ist einer von unendlich vielen Punkten der Eben
Die Punkte ablesen, sodass du zwei Spannvektoren deiner Ebene und einen Stützvektor deiner Ebene bestimmen kann, schon hast du die Ebenengleichung in Parameterform.
Zu E1 steht in meinem Lösungsbuch (0|0|0) + r (1|0|0) + s (0|1|0) könntest du vielleicht erklären, wie man darauf kommt, vor allem warum der Ursprung als Ortsvektor genutzt wird?
Also E1:x = (0|0|0) + r (1|0|0) + s (0|1|0)
Könntest du vielleicht kurz erklären warum es unbedingt der Ortsvektor (0|0|0) sein muss? Weil für E3 bei der gleichen Aufgabe 4a) wurde (0|0|0) nicht als Ortsvektor genommen, aber bei E2 schon, wie bei E1 auch ....